Tutorial 1 - Modelos ópticos

Este es un tutorial para utilizar las principales librerías del paquete empylib. Estas son:

• Funciones básicas en empylib.

• nklib para estimación de índices de refracción.

• waveoptics para cálculo de propiedades de reflectancia y transmitancia de ondas electromagnéticas.

• miescattering para cálculo scattering y absorción de luz

• rad_transfer para simulaciones de transferencia de energía radiativa.

Primero, importamos los paquetes estandar de numpy y matplotlib

import numpy as np
import matplotlib.pyplot as plt

Conversión de unidades

import empylib as em

La librería empylib cuenta con la función convert_units(x, x_in, to) para convertir unidades. Los parámetros de entrada son:

• x: lista de valores a convertir (formato ndarray)

• x_in: unidad de la lista de valores (formato string)

• to: unidad a convertir (formato string)

La función retorna la lista de valores en x convertido a la unidad to.

Como opciones, la función permite convertir las siguientes unidades:

• Nanometros (\(\lambda\)) : 'nm'

• Micrometros (\(\lambda\)) : 'um'

• Centímetros recíprocos : 'cm^-1'

• Frecuencia (\(\nu\)) : 'Hz'

• Frecuencia angular (\(\omega\)) : 'rad/s'

• Electron volts (\(E_{\hbar\omega}\)) : 'eV'

Por ejemplo, realicemos la conversión del espectro \(\lambda \in [0.3,1.0]\) \(\mu\)m considerando 8 puntos igualmente espaciados, a unidades de eV.

lam = np.linspace(0.3,1.0,8)   # espectro de longitudes de onda en um
print('longitudes de onda en um:\n', lam)

lam_in_eV = em.convert_units(lam,'um','eV') # convertimos lam a unidades de eV
print('longitudes de onda en eV:\n', lam_in_eV)

longitudes de onda en um:
 [0.3 0.4 0.5 0.6 0.7 0.8 0.9 1. ]
longitudes de onda en eV:
 [4.13280655 3.09960491 2.47968393 2.06640327 1.77120281 1.54980245
 1.37760218 1.23984196]

# revertimos el proceso para recuperar las longitudes de onda en um
lam_in_um = em.convert_units(lam_in_eV,'eV','um') # convertimos lam a unidades de eVicrones
print('longitudes de onda en um:\n', lam_in_um)

longitudes de onda en um:
 [0.3 0.4 0.5 0.6 0.7 0.8 0.9 1. ]

Índices de refracción (nklib)

import empylib.nklib as nk

Índices de refracción tabulados

La librería empylib.nklib contiene una serie de funciones para determinar el coeficiente de refracción complejo, \(N = n + i\kappa\).

Entre la lista de materiales disponibles tenemos:

• Agua (H2O)

• Oro (gold)

• Plata (silver)

• Cobre (Cu)

• Aluminio (Al)

• Silice (SiO2)

• Silicio (Si)

• Dióxido de Titanio (TiO2)

Para utilizar las funciones debemos, primero, generar un arreglo con las longitudes de onda que deseamos graficar, y luego evaluar la función para determinar el índice de refracción.

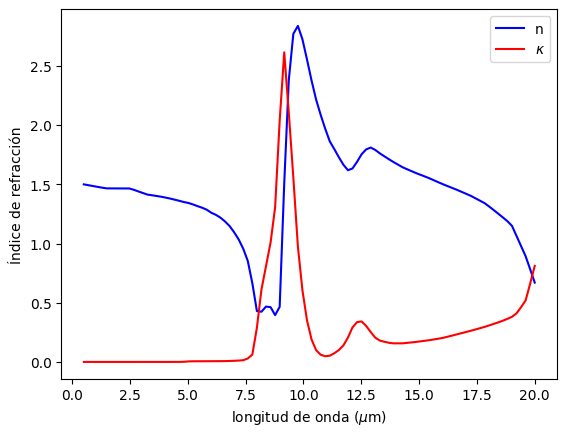
Por ejemplo, supongamos que necesitamos el índice de refracción del sílice en el espectro \(\lambda\in[0.5,20]\) \(\mu\)m.

lam = np.linspace(0.5,20,100)   # arreglo de 100 datos entre 0.5 y 5.0 micrones
N   = nk.SiO2(lam)              # índice de refracción del sílice

# graficamos el índice de refracción
plt.plot(lam, N.real,'-b', label = 'n')
plt.plot(lam, N.imag,'-r', label = '$\kappa$')
plt.xlabel('longitud de onda ($\mu$m)')
plt.ylabel('Índice de refracción')
plt.legend()
plt.show()

También podemos extraer un valor puntual, para una longitud de onda específica. Por ejemplo, si necesitamos el índice de refracción del aluminio en \(\lambda = 0.5\) \(\mu\)m, hacemos:

lam0 = 0.5
nk.Al(lam0)

(0.8125653662219986+6.048056732947395j)

Modelos de Drude y Lorentz

La librería empylib.nklib también posee funciones para determinar el índice de refracción a partir de modelos de Drude y Lorentz.

Notar que estas funciones entregan el índice de refracción. Para esto, cada función toma el modelo de Drude o Lorentz para determinar la constante dieléctrica \(\varepsilon\), según lo visto en clases. Luego el índice de refracción se determina a partir de \(\sqrt{\varepsilon}\)

Cada modelo requiere una serie de parámetros. Podemos verificar los parámetros requeridos mediante la función help.

help(nk.lorentz)

Help on function lorentz in module empylib.nklib:

lorentz(epsinf, wp, wn, gamma, lam)
    Refractive index from Lorentz model
    
    Parameters
    ----------
    epsinf : float
        dielectric constant at infinity.
    wp : float
        Plasma frequency, in eV (wp^2 = Nq^2/eps0 m).
    wn : float
        Natural frequency in eV
    gamma : float
        Decay rate in eV
    lam : linear np.array
        wavelength spectrum in um
    
    Returns
    -------
    complex refractive index

Como vemos la función lorentz requiere los parámetros \(\omega_p\), \(\omega_n\) y \(\Gamma\) en unidades de eV, además de \(\varepsilon_\infty\). Por último, la función también requiere el espectro de longitudes de onda en unidades de micrones (um) a partir de la variable lam.

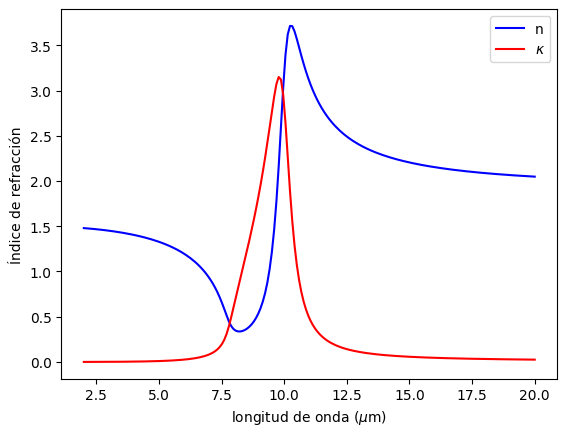
En el siguiente ejemplo, graficaremos el modelo de Lorentz para \(\lambda\in[2,20]\) \(\mu\)m, considerando los siguientes parámetros:

• \(\omega_n = 0.124\) eV (\(\approx 10\) \(\mu\)m)

• \(\omega_p = 0.150\) eV

• \(\Gamma = 0.01\) eV

• \(\varepsilon_\infty = 2.25\)

Índice de refracción según modelo de Lorentz

lam = np.linspace(2,20,200)   # arreglo de 100 datos entre 0.5 y 5.0 micrones

wn = 0.124  # Frecuencia natural (eV)
wp = 0.150  # Frecuencia wp (eV)
T = 0.01    # Taza de decaimiento (eV)
eps0 = 2.25

Nlorentz   = nk.lorentz(eps0,wp,wn,T,lam)  # índice de refracción modelo de drude

# graficamos el índice de refracción
plt.plot(lam, Nlorentz.real,'-b', label = 'n')
plt.plot(lam, Nlorentz.imag,'-r', label = '$\kappa$')
plt.xlabel('longitud de onda ($\mu$m)')
plt.ylabel('Índice de refracción')
plt.legend()
plt.show()

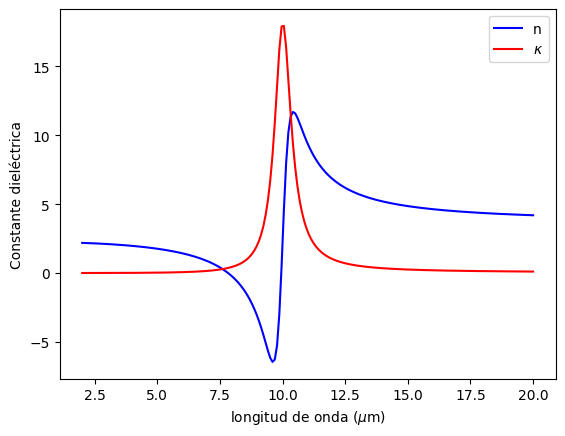
Constante dieléctrica según modelo de Lorentz

eps_lorentz = Nlorentz**2

# graficamos el índice de refracción
plt.plot(lam, eps_lorentz.real,'-b', label = 'n')
plt.plot(lam, eps_lorentz.imag,'-r', label = '$\kappa$')
plt.xlabel('longitud de onda ($\mu$m)')
plt.ylabel('Constante dieléctrica')
plt.legend()
plt.show()

lam = np.linspace(0.3,8,200)   # arreglo de 100 datos entre 0.5 y 5.0 micrones

eps0=10
wn = 0.289    # Frecuencia natural (eV)
wp = 0.15*wn  # Frecuencia wp (eV)
T = 0.01      # Taza de decaimiento (eV)

nkco2 = nk.lorentz(eps0,wp,wn,T,lam)
epsco2 = nkco2**2

plt.plot(lam, epsco2.real,'r')
plt.plot(lam, epsco2.imag,'b')
plt.show()

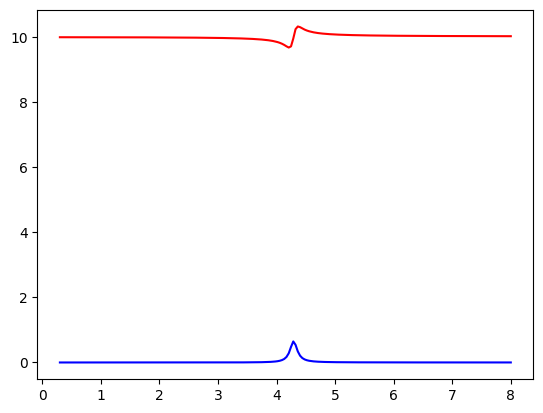
Constante dieléctrica del agua modelo de Lorentz

Ahora, generemos la constante dieléctrica del agua a partir del modelo de Lorentz.

En el caso del agua, tenemos dos modos de vibración (referencia). Así, el modelo de Lorentz es:

\[\begin{equation*} \varepsilon = \varepsilon_\infty + \frac{\omega_{p_1}^2}{\omega_{n_1}^2 - \omega^2 - i\Gamma \omega} + \frac{\omega_{p_2}^2}{\omega_{n_2}^2 - \omega^2 - i\Gamma \omega}, \end{equation*}\]

donde \(\omega_{n_1}\) y \(\omega_{n_2}\) son las frecuencias naturales de los modos de vibración.

Como aproximación consideramos:

• \(\Gamma = 0.01\) eV

• \(\omega_{p_i} = 0.2\omega_{n_i}\) eV

• \(\varepsilon_\infty\) = 2.0

# a partir del video tenemos
modos = np.array([3412, 1691])            # unidades de cm^(-1)
wn = em.convert_units(modos,'cm^-1','eV') # frecuencias naturales en eV
wn

array([0.42303408, 0.20965728])

Generamos nuestro modelo, y graficamos para \(\lambda\in[2,10]\) \(\mu\)m

# generamos modelo del agua 

wp = 0.2*wn
gamma = 0.01
epsinf = 2

lam = np.linspace(2.0,10,100)   # espectro de longitudes de onda
# constante dielectrica del agua
eps_agua = epsinf + nk.lorentz(0, wp[0], wn[0], gamma, lam)**2 \
                  + nk.lorentz(0, wp[1], wn[1], gamma, lam)**2

# graficamos el índice de refracción
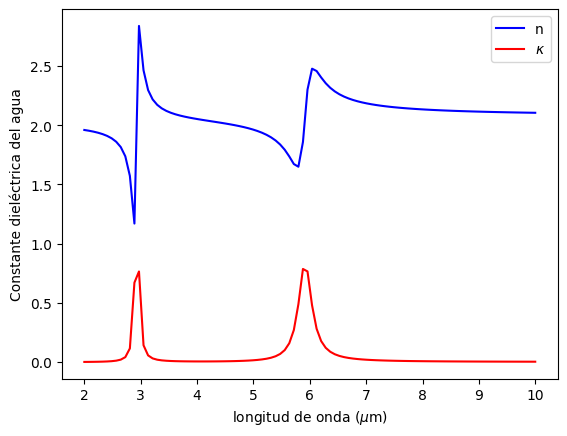
plt.plot(lam, eps_agua.real,'-b', label = 'n')
plt.plot(lam, eps_agua.imag,'-r', label = '$\kappa$')
plt.xlabel('longitud de onda ($\mu$m)')
plt.ylabel('Constante dieléctrica del agua')
plt.legend()
plt.show()

Reflexión/Transmissión (waveoptics)

import empylib.waveoptics as wv

La librería empylib.waveoptics contiene funciones para calcular los coeficientes de Fresnel y Flujo de energía de la porción transmitida y reflejada de la luz incidente.

• interface para una interface simple

• multilayer para multicapas de película delgada

• incoh_multilayer para multicapas de película delgada ignorando fenómenos de interferencia (luz incoherente)

Luz incidente en una interface (interface)

Esta función permite determinar los coeficientes de Fresnel y flujo de energía para la onda reflejada y transmitida a través de una interface. La función toma 4 argumentos:

• theta: ángulo de incidencia (en radianes)

• n1: índice de refracción del medio sobre la interface

• n2: índice de refracción del medio bajo la interface

• pol: Polarización de la onda incidente ('TM' o 'TE' )

La función necesita como mínimo 3 argumentos: theta, n1, n2. En ese caso, pol= 'TM' por defecto.

En el orden respectivo, el output es:

• Reflectividad R y Tranmisividad T

• coefientes de Fresnel de reflexión r y transmisión t.

En el siguiente ejemplo analizaremos una interface que separa aire (índice de refracción 1.0) y un metal de Drude con \(\omega_p = 3.1\) eV (aprox 0.4 \(\mu\)m), \(\Gamma = 0.01\) eV y \(\varepsilon_\infty = 1.0\). El ángulo de incidencia es \(\theta_i = 30°\).

Notar que n1=1.0 es un valor float unidimencional, mientras que n2 es un arreglo en el espectro \(\lambda \in [0.3,1.0]\) \(\mu\)m. En este caso, la función repite n1=1.0 por cada valor espectral de n2. En el caso que n1 y n2 sean un arreglo, ambos deben tener igual dimención.

R, T = wv.interface(0,1.0,2.0, pol='TM')[:2] # extraer los dos primeros elementos de la función
print(R, T)

[0.11111111] [0.88888889]

theta = np.radians(30)         # Angulo de incidencia (radianes)
lam = np.linspace(0.3,1.0,100) # Espectro de longitudes de onda

# Modelo de Drude
epsinf = 1.0 
wp = 2.1      # en eV (aproximadamente 0.4 micrones)
gamma = 0.01  # en eV

n2 = nk.drude(epsinf,wp,gamma,lam) # índice de refracción
n1 = 1.0

# Coeficientes de Fresnel y flujo de energia
Rp, Tp, rp, tp = wv.interface(theta,n1,n2, pol='TM') # polarizacion TM
Rs, Ts, rs, ts = wv.interface(theta,n1,n2, pol='TE') # polarizacion TE

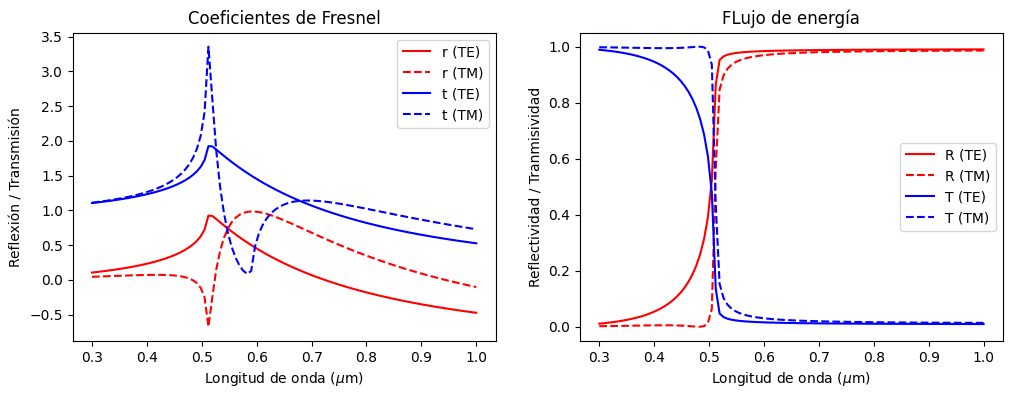
Abajo graficamos los coeficientes de Fresnel a la izquierda (solo la parte real) y el flujo de energía a la derecha. Notar como la reflectividad aumenta para \(\lambda < 2\pi c_0/\omega_p\)

fig, ax = plt.subplots(1,2)
fig.set_size_inches(12,4)
ax[0].plot(lam,rs.real, '-r',label = 'r (TE)')
ax[0].plot(lam,rp.real,'--r',label = 'r (TM)')
ax[0].plot(lam,ts.real, '-b',label = 't (TE)')
ax[0].plot(lam,tp.real,'--b',label = 't (TM)')
ax[0].set_title('Coeficientes de Fresnel')
ax[0].set_xlabel('Longitud de onda ($\mu$m)')
ax[0].set_ylabel('Reflexión / Transmisión')
ax[0].legend()

ax[1].plot(lam,Rs, '-r',label = 'R (TE)')
ax[1].plot(lam,Rp,'--r',label = 'R (TM)')
ax[1].plot(lam,Ts, '-b',label = 'T (TE)')
ax[1].plot(lam,Tp,'--b',label = 'T (TM)')
ax[1].set_title('FLujo de energía')
ax[1].set_xlabel('Longitud de onda ($\mu$m)')
ax[1].set_ylabel('Reflectividad / Tranmisividad')
ax[1].legend()
plt.show()

Luz incidente en arreglos multicapas (multilayer)

Esta función permite determinar los coeficientes de Fresnel y flujo de energía para la onda reflejada y transmitida a través de un arreglo de multicapas. La función toma 5 argumentos:

• lam: Espectro de longitudes de onda (en \(\mu\)m)

• tt: ángulo de incidencia (en radianes)

• N: arreglo tuple con índices de refracción de cada capa + medio superior e inferior al arreglo

• d: arreglo tuple con espesores de cada capa (en micrones)

• pol: Polarización de la onda incidente ('TM' o 'TE' )

La función necesita como mínimo 4 argumentos: lam, tt N y d. En ese caso, pol= 'TM' por defecto.

En el orden respectivo, el output es:

• Reflectividad R y Tranmisividad T

• coefientes de Fresnel de reflexión r y transmisión t.

Los elementos de N y d, deben estar ordenados según la dirección de la onda incidente. Por ejemplo, si consideramos:

• luz incidente (\(\theta_i = 45°\), \(\lambda\in[0.3,0.8]\) \(\mu\)m)

• Propagandose en aire (\(N_1 = 1.0\)),

• La luz incide sobre una película de espesor \(d = 300\) nm e índice de refracción \(N_2 = 1.5\).

• La película está depositada sobre un sustrato con índice de refracción \(N_3 = 5.0 + 3i\):

lam = np.linspace(0.3,0.8,100)  # espectro de longitudes de onda (um)
theta = np.radians(45)
N1 = 1.0 # aire
N2 = 1.5 # capa intermedia
N3 = 5.0 + 3j

N = (N1, N2, N3) # indices de refracción (above, mid, below)
d = 0.3          # 300 nm de espesor para capa intermedia

Rp, Tp, rp, tp = wv.multilayer(lam,theta, N, d, pol='TM')
Rs, Ts, rs, ts = wv.multilayer(lam,theta, N, d, pol='TE')

Notar que len(d) = len(N) - 2, debido a que los índices superior e inferior corresponden a los medios semi-infinitos sobre y bajo la capa.

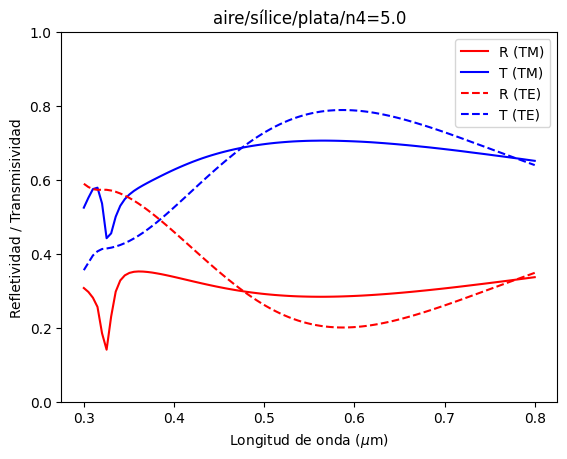
Por ejemplo, si ahora queremos determinar la respuesta óptica de un arreglo de una capa delgada de sílice (\(d_1 = 100\) nm) sobre una capa de plata (\(d_2 = 10\) nm), sobre un sustrato con índice de refracción \(n_{back} = 5.0\)

lam = np.linspace(0.3,0.8,100)  # espectro de longitudes de onda (um)
theta = np.radians(45)

Nfront = 1.0                 # índice de refracción medio superior
N1     = nk.SiO2(lam)        # índice de refracción sílice
N2     = nk.silver(lam)      # índice de refracción plata
Nback  = 5.0                 # índice de refracción medio inferior
N = (Nfront, N1, N2, Nback)  # indices de refracción (above, mid, below)

d = (0.100, 0.010) # espesor para sílice y plata (en ese orden)

Rp, Tp, rp, tp = wv.multilayer(lam,theta, N, d, pol='TM')
Rs, Ts, rs, ts = wv.multilayer(lam,theta, N, d, pol='TE')

# Graficamos el flujo de energía
plt.plot(lam,Rp,'-r',label='R (TM)')
plt.plot(lam,Tp,'-b',label='T (TM)')
plt.plot(lam,Rs,'--r',label='R (TE)')
plt.plot(lam,Ts,'--b',label='T (TE)')
plt.title('aire/sílice/plata/n4=5.0')
plt.xlabel('Longitud de onda ($\mu$m)')
plt.ylabel('Refletividad / Transmisividad')
plt.ylim(0,1)
plt.legend()
plt.show()

Luz incoherente en arreglos multicapas (incoh_multilayer)

Esta función es similar a multilayer pero para una fuente de luz incoherente. Considera los mismos 5 argumentos de multilayer con un argumento adicional coh_length para condicionar la longitud de coherencia (en \(\mu\)m). Por defecto, coh_length = 0

Debido a que la función es para luz incoherente, el output es:

• Reflectividad R y Tranmisividad T

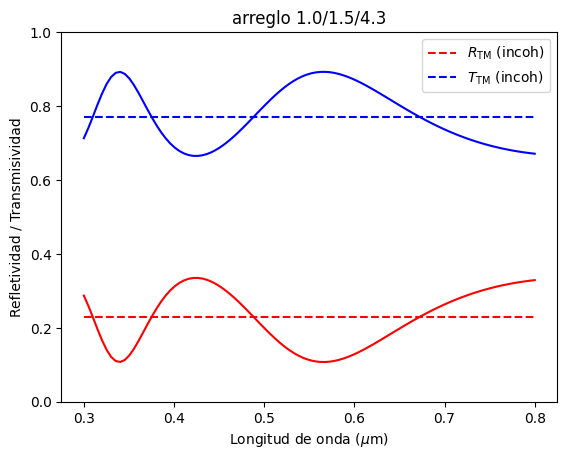
Por ejemplo, evaluemos el ejemplo de la clase 2 (\(n_\mathrm{front}= 1.0\), \(n_\mathrm{layer}= 1.5\), \(n_\mathrm{back} = 4.3\)), considerando una capa de espesor \(d = 300\) nm, y \(\theta_i = 30°\)

lam = np.linspace(0.3,0.8,100)  # espectro de longitudes de onda (um)
theta = np.radians(30)          # ángulo de incidencia

Nfront = 1.0                 # índice de refracción medio superior
N1     = 1.5                 # índice de refracción capa delgada
Nback  = 4.3                 # índice de refracción medio inferior
N = (Nfront, N1, Nback)      # indices de refracción (above, mid, below)

d = 0.3                      # espesor capa intermedia (um)

Rp_incoh, Tp_incoh = wv.incoh_multilayer(lam,theta, N, d, pol='TM') # caso luz incoherente

# Graficamos el flujo de energía
plt.plot(lam,Rp_incoh,'--r',label='$R_\mathrm{TM}$ (incoh)')
plt.plot(lam,Tp_incoh,'--b',label='$T_\mathrm{TM}$ (incoh)')
plt.title('arreglo 1.0/1.5/4.3')
plt.xlabel('Longitud de onda ($\mu$m)')
plt.ylabel('Refletividad / Transmisividad')
plt.ylim(0,1)
plt.legend()

# comparamos con el caso luz coherente
Rp, Tp = wv.multilayer(lam,theta, N, d, pol='TM')[:2]
plt.plot(lam,Rp,'-r',label='$R_\mathrm{TM}$ (coh)')
plt.plot(lam,Tp,'-b',label='$T_\mathrm{TM}$ (coh)')

plt.show()

En el límite de solo una interface, interface, multilayer y incoh_multilayer entregan el mismo resultado

lam = 0.5                # longitud de onda en micrones
theta = np.radians(30)   # ángulo de incidencia (en radianes)                    

N = (1.0, 1.5)  # interface aire/silice
d = ()          # sin espesores (solo una interface)

print('interface:\t\t R = %.3f, T = %.3f' % wv.interface(theta,N[0],N[1])[:2])
print('multilayer:\t\t R = %.3f, T = %.3f' % wv.multilayer(lam,theta,N,d)[:2])
print('incoh_multilayer:\t R = %.3f, T = %.3f' % wv.incoh_multilayer(lam,theta,N,d))

interface:		 R = 0.025, T = 0.975
multilayer:		 R = 0.025, T = 0.975
incoh_multilayer:	 R = 0.025, T = 0.975

Scattering de mie (miescattering)

import empylib.miescattering as mie

En esta librería, la función principal es scatter_efficiency, que permite determinar las secciones transversales de scattering, absorción y extinción para una partícula esférica de diámetro \(D\).

Los pámetros de entrada son:

• lam: Espectro de longitudes de onda (en \(\mu\)m)

• Nh: Índice de refracción del medio circundante

• Np: Índice de refracción de la partícula

• D: Diámetro de la partícula (en \(\mu\)m)

Los parámetros de salida son

• Qext: coeficiente de extinción (\(C_\mathrm{ext}/\pi R^2\))

• Qsca: coeficiente de scattering (\(C_\mathrm{sca}/\pi R^2\))

• gcos: parámetro de asimetría

Los coeficientes de extinción (\(Q_\mathrm{ext}\)) y scattering (\(Q_\mathrm{sca}\)) se relacionan con las respectivas secciones transversales por \(C_\mathrm{ext} = Q_\mathrm{ext}A_c\), \(C_\mathrm{sca} = Q_\mathrm{sca}A_c\), donde \(A_c = \pi D^2/4\) es la sección transversal de la esfera.

La sección transversal de absorción (\(C_\mathrm{abs}\)), se determina por \(C_\mathrm{abs} = C_\mathrm{ext} - C_\mathrm{sca}\)

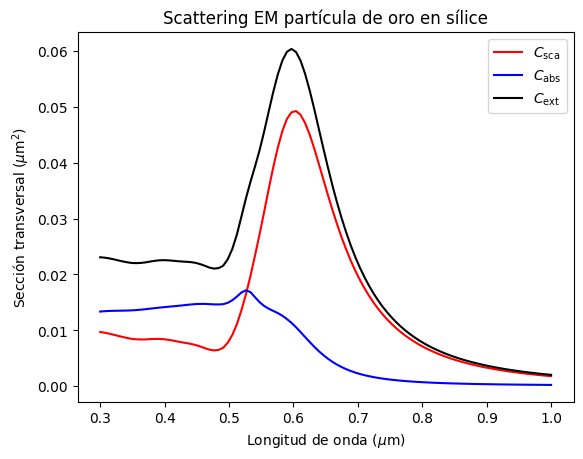
En el ejemplo de abajo, calculamos la \(C_\mathrm{abs}\), \(C_\mathrm{sca}\) y \(C_\mathrm{ext}\) para una partícula de oro de \(D = 100\) nm de diámetro, alojada de sílice. El espectro considerado es \(\lambda\in[0.3,1.0]\) \(\mu\)m

lam = np.linspace(0.3,1.0,100) #espectro de longitudes de onda (arreglo de 100 puntos entre 0.3 y 1.0 micrones)
Nh = nk.SiO2(lam) # índice de refracción medio circundante
Np = nk.gold(lam) # índice de refracción partícula
D = 0.100         # diámetro de la partícula (micrones)

# determinamos parámetros de eficiencia
qext, qsca = mie.scatter_efficiency(lam,Nh,Np,D)[:2]

# convertimos los resultados a secciones transversales
Ac = np.pi*D**2/4 # sección transversal de la partícula
Csca = qsca*Ac
Cext = qext*Ac
Cabs = Cext - Csca

# graficamos los resultados
plt.plot(lam,Csca,'-r',label='$C_\mathrm{sca}$')
plt.plot(lam,Cabs,'-b',label='$C_\mathrm{abs}$')
plt.plot(lam,Cext,'-k',label='$C_\mathrm{ext}$')
plt.xlabel('Longitud de onda ($\mu$m)')
plt.ylabel('Sección transversal ($\mu$m$^2$)')
plt.title('Scattering EM partícula de oro en sílice')
plt.legend()
plt.show()

Transporte Radiativo (rad_transfer)

import empylib.rad_transfer as rt

Para transporte radiativo tenemos dos librerías:

• rad_transfer con funciones para cálculos simples (como Beer-Lambert)

• iadpython para simulaciones de scattering multiple

Beer-Lambert (T_beer_lambert)

La función T_beer_lambert de la librería empylib.rad_transfer permite un rápido cálculo de la transmisivitidad a través de un medio de espesor \(d\) con incrustaciones.

La función requiere los siguientes parámetros de entrada:

• lam: Espectro de longitudes de onda (en \(\mu\)m)

• theta: Ángulo de incidencia (en radianes)

• tfilm: Espesor del material (en mm)

• N: Índice de refracción del medio superior, material intermedio, y medio inferior (arreglo tuple len(N) = 3)

• fv: Fracción de volumen de las incrustaciones (0.01 corresponde a 1% v/v)

• D: Diámetro de la partícula (en \(\mu\)m)

• Np: Índice de refracción de las partículas (se debe cumplir la condición: len(Np) = len(lam))

Los parámetros de salida (en orden) son:

• Ttot : Transmisividad total

• Rtot : Reflectividad total

• Tspec: Transmisividad especular

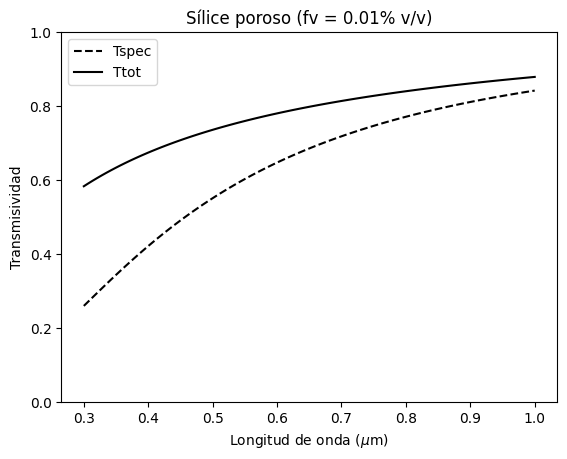
En el siguiente ejemplo, consideramos una película de sílice de espesor \(1.0\) mm, con porosidad de 0.01% donde los poros tienen un de diámetro \(D = 200\) \(\mu\)m (\(N_{poro} = 1.0\)). Los medios superior e inferior corresponden a aire. La luz incide en dirección \(\theta_i = 0°\).

lam = np.linspace(0.3,1.0,100)  # espectro de longitudes de onda (en micrones)
theta = np.radians(0)           # 30 grados en radianes
tfilm = 1.0                     # espesor en mm
N = (1.0,nk.SiO2(lam),1.0)      # indice de refracción superior, intermedio e inferior
fv = 0.0001                     # fracción de volúmen de los poros
D = 0.2                         # diámetro de los poros (micrones)
Np = 1.0                        # índice de refracción de las incrustaciones

Ttot, Rtot, Tspec = rt.T_beer_lambert(lam,theta,tfilm,N,fv,D,Np)

plt.plot(lam,Tspec,'--k',label = 'Tspec')
plt.plot(lam,Ttot,'-k',label = 'Ttot')
plt.xlabel('Longitud de onda ($\mu$m)')
plt.ylabel('Transmisividad')
plt.title(r'Sílice poroso (fv = 0.01% v/v)')
plt.legend()
plt.ylim(0,1)
plt.show()

Scattering multiple (adm_sphere)

La función adm_sphere de la librería empylib.rad_transfer permite el cálculo de scattering múltiple en una película con incrustaciones entre dos medios semi-infinitos. La función utliza la librería iadpython la cual utiliza el adding doubling method (adm) para resolver la RTE numéricamente.

La función requiere los siguientes parámetros de entrada:

• lam: Espectro de longitudes de onda (en \(\mu\)m)

• theta: Ángulo de incidencia (en radianes)

• tfilm: Espesor del material (en mm)

• N: Índice de refracción del medio superior, material intermedio, y medio inferior (arreglo tuple len(N) = 3)

• fv: Fracción de volumen de las incrustaciones (0.01 corresponde a 1% v/v)

• D: Diámetro de la partícula (en \(\mu\)m)

• Np: Índice de refracción de las partículas (se debe cumplir la condición: len(Np) = len(lam))

Los parámetros de salida son:

• Ttot: Transmisividad total

• Rtot: Reflectividad total

• Tspec: Transmisividad specular

• Rspec: Reflectividad specular

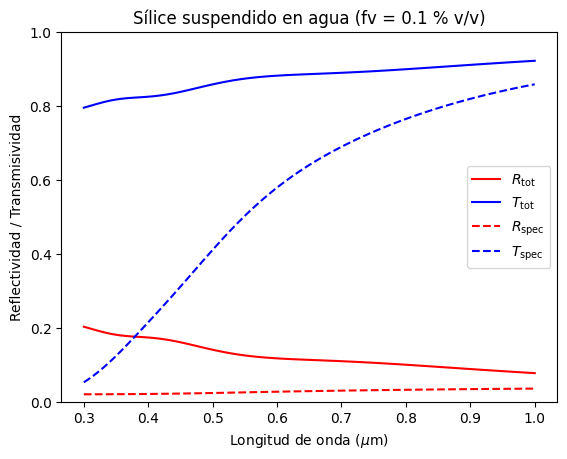
En el ejemplo, se modela una pekícula de agua con partículas de sílice suspendidas con las siguientes características:

• Espesor de la película de agua: 1 mm

• concentración de partículas de sílice: 0.1 % v/v

• Tamaño de las partículas: \(0.3\) \(\mu\)m

• Espectro \(\lambda\in[0.3,1.0]\) \(\mu\)m

lam = np.linspace(0.3,1.0,100) # espectro de longitudes de onda
tfilm = 1                      # espesor en mm
N = (1.0,1.33,1.0)             # indice de refracción superior, intermedio e inferior
fv = 0.001                     # fracción de volúmen de los poros
D = 0.3                        # diámetro de los poros (micrones)
Np = nk.SiO2(lam)              # índice de refracción partícula

Ttot, Rtot, Tspec, Rspec = rt.adm_sphere(lam,tfilm,N,fv,D,Np)

plt.plot(lam,Rtot,'-r',label='$R_\mathrm{tot}$')
plt.plot(lam,Ttot,'-b',label='$T_\mathrm{tot}$')
plt.plot(lam,Rspec,'--r',label='$R_\mathrm{spec}$')
plt.plot(lam,Tspec,'--b',label='$T_\mathrm{spec}$')
plt.xlabel('Longitud de onda ($\mu$m)')
plt.ylabel('Reflectividad / Transmisividad')
plt.title(r'Sílice suspendido en agua (fv = %.1f %% v/v)' % (fv*100))
plt.legend()
plt.ylim(0,1)
plt.show()