Transporte Radiativo

5. Transporte Radiativo#

5.1. Introducción#

En la unidad 2 revisamos el efecto de interferencia en películas de espesor finito, y como está daba lugar a los patrones caractéristicos observados en derrames de aceites en agua, lentes y discos compactos.

Si, teóricamente, el efecto de interferencia ocurre cada vez que tenemos un tercer material intercalado entre dos materiales (iguales o diferentes). ¿Porqué no visualizamos este efecto en ventanas u otros materiales de gran espesor?

5.2. Coherencia de la luz e interferencia#

Para entender esto, primero debemos revisar la distribución espectral de fuentes reales de luz.

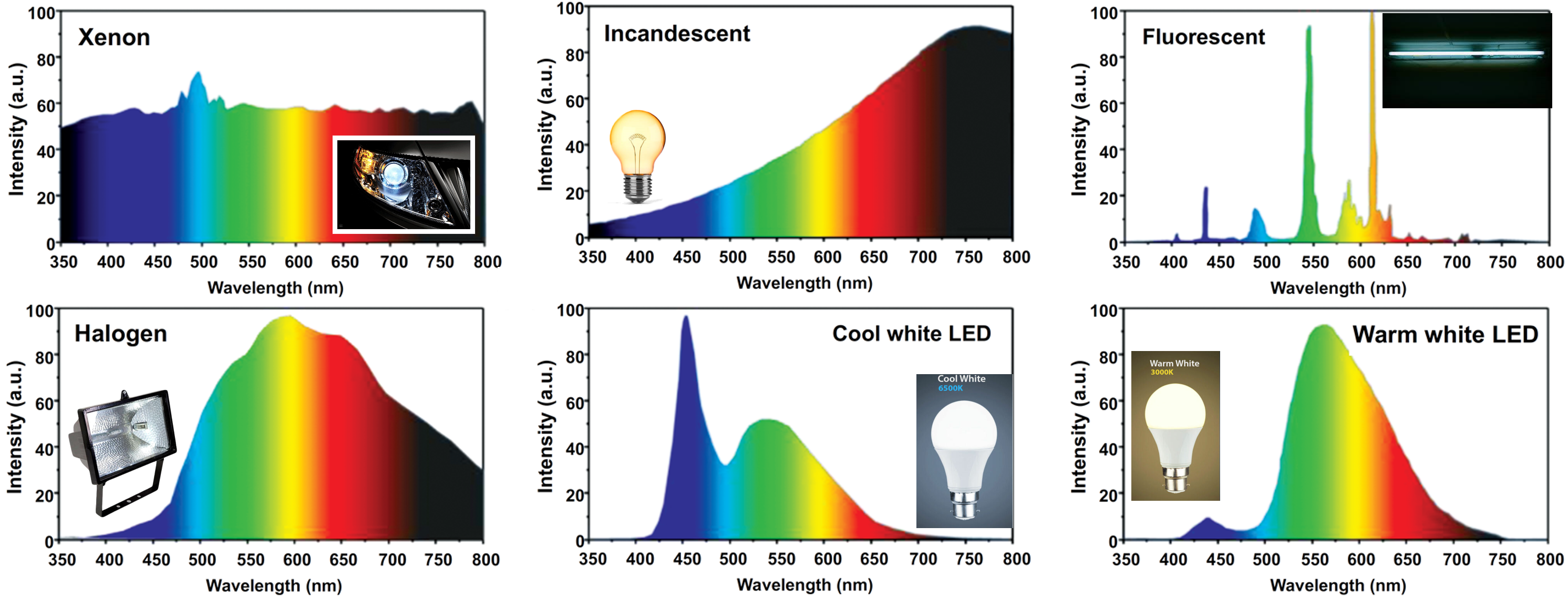
Como vemos, una fuente emite luz en varias longitudes de onda y a distinta intensidad. Así, las ondas emitidas se superponen, generando una onda resultante con una forma distinta a $e^{i(\vec{k}\cdot\vec{r} -\omega t)}$.

Consideremos, por ejemplo, una fuente de luz con una distribución espectral normal, centrada en $\lambda_0$ y con una desviación estandar $\pm\sigma_\lambda\lambda_0$, con $\sigma_\lambda \in [0,1]$. Imaginemos esta fuente como $N$ emisores, donde cada emisor $j$ emite una onda electromagnéticas con longitud de onda $\lambda \pm\Delta \lambda_j$, donde $\Delta \lambda_j$ es escogido aleatoriamente a partir de la distribución normal.

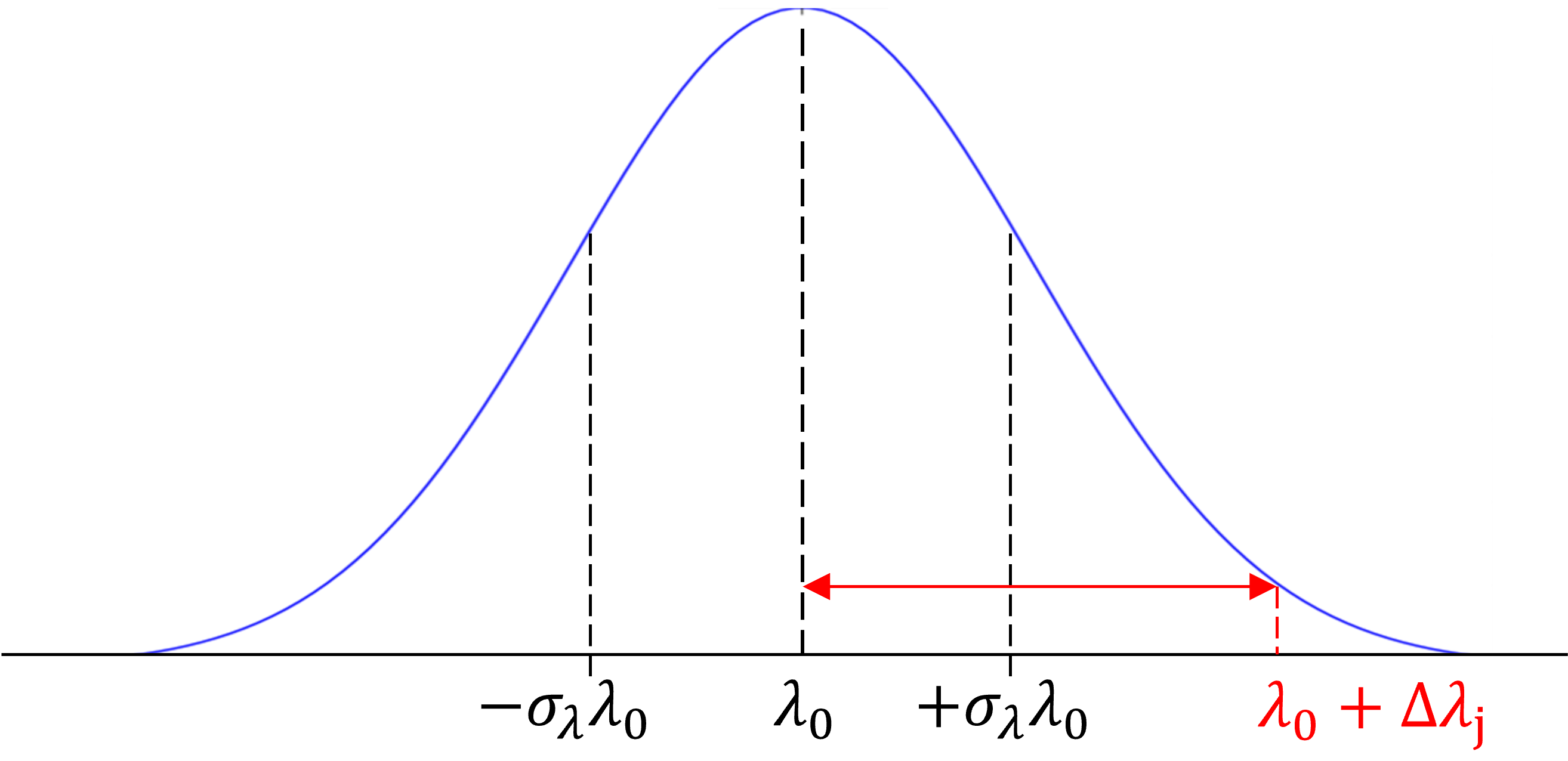
Asumiendo ondas en el aire en dirección $\hat{k} = \hat{x}$, el campo eléctrico resultante esta dado por la suma de ondas EM, cada una con una amplitud está dada por la distribución espectral:

\[\begin{equation*} \vec{E}_\mathrm{tot} = \sum_j^N E_0f(\lambda_j)e^{i\left(k_jx - \omega_j t\right)} \hat{z}, \end{equation*}\]

donde $k_j = \frac{2\pi}{\lambda_j}$, $\omega_j = c_0k_j$ y

\[\begin{equation*} f(\lambda_j) = \frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{1}{2}\left(\frac{\lambda_j - \lambda_0}{\sigma}\right)} \end{equation*}\]

es la distribución normal centrada en $\lambda_0$ y con desviación estandar $\sigma$.

Analicemos el comportamiento de $\vec{E}_\mathrm{tot} /E_0$ para $\lambda_0 = 500$ nm

Note como la onda resultante se desvanece en los extremos a medida que $\sigma$ aumenta.

5.2.1. Longitud de coherencia#

Definimos como longitud de coherencia, $l_c$, a la longitud donde la onda electromagnética resultante mantiene correlación entre las fases. Dos puntos en una paquete de onda separados a una distancia mayor a $l_c$ son incoherentes, es decir, no están correlacionados

Esquema de un paquete de onda emitido por una fuente con longitud de coherencia $l_c$

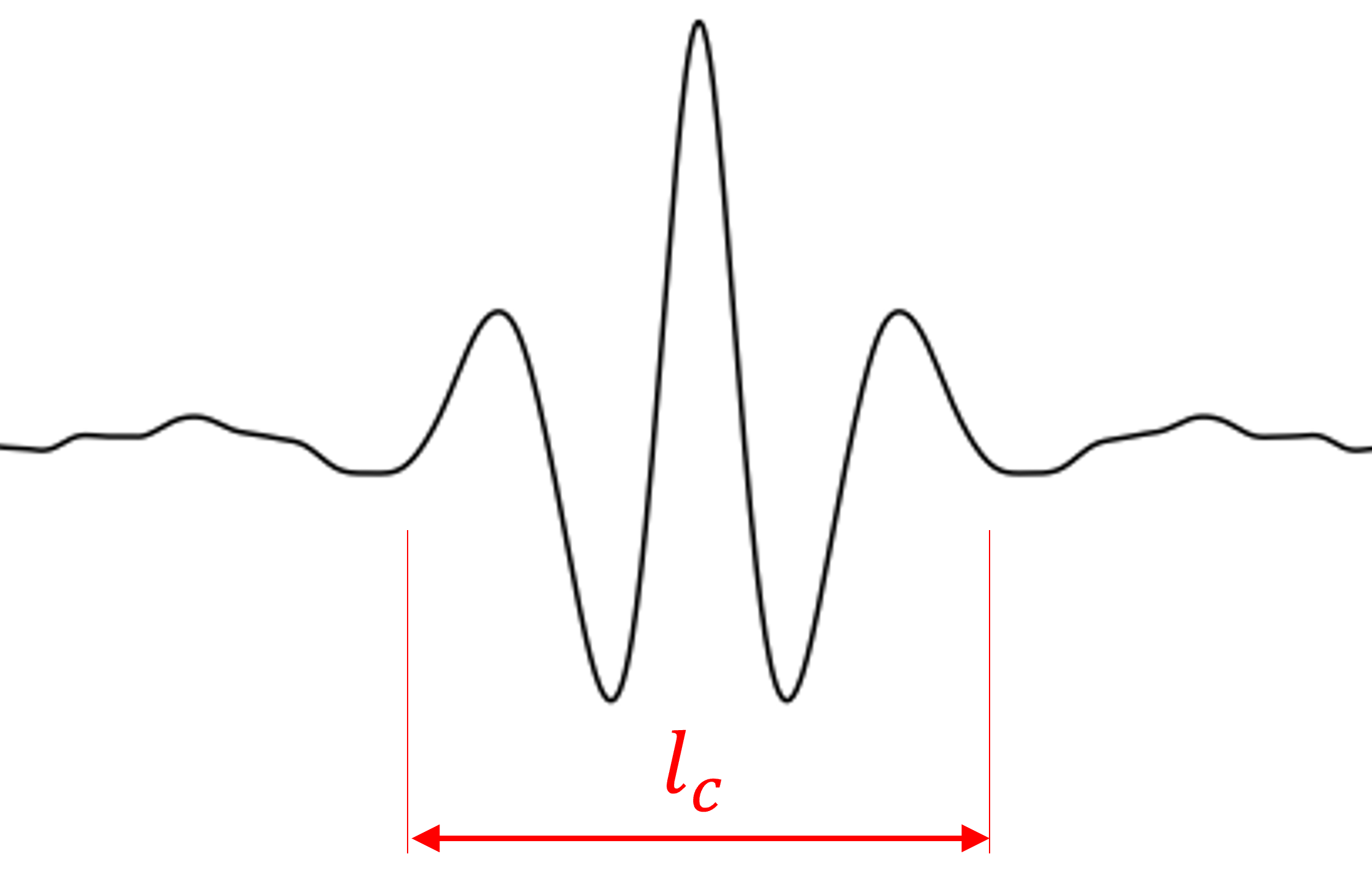
La relación entre $l_c$, la longitud de onda central $\lambda$ y el ancho de banda $\Delta\lambda$ está dado, aproximadamente, por la relación:

\[\begin{equation*} l_c \approx \frac{\lambda^2}{n\Delta \lambda}, \end{equation*}\]

donde $n$ es el indice de refracción del medio donde se propaga la luz.

Por ejemplo, para lasers He-Ne (laser rojo) $l_c\approx 0.2 - 100$ m.

Para radiación emitida por un cuerpo a temperatura $T$, la longitud de coherencia está dada por:

\[\begin{equation*} l_c T = 2167.8~\mathrm{\mu m~K} \end{equation*}\]

Así, por ejemplo, la radiación solar ($T \approx 5800~\mathrm{K}$) tiene una longitud de coherencia, $l_c \approx 370~\mathrm{nm}$

¿Qué relevancia tiene la longitud de coherencia en los fenómenos vistos hasta ahora?

5.2.2. Régimen de trasporte de luz#

Los fenómenos de interferencia descritos en las unidades anteriores asumen ondas distribuidas infinitamente en el espacio. Así, en el fenómeno de película delgada (por ejemplo), la interferencia ocurre entre la onda incidente y las que son reflejadas en la interfaz bajo y sobre la película.

Sin embargo, la superposición de dos paquetes de ondas con longitud de coherencia $l_c$ no generará interferencia si la distancia entre ellos es mayor a $l_c$.

En otras palabras, el fenómeno de interferencia solo existe si el paquete de onda interfiere consigo mismo. Así, podemos concluir que los fenómenos de interferencia en películas de espesor $d$ no serían visibles si $d > l_c$.

Propagación de una onda a través de una película de espesor $d$, con $l_c < d$

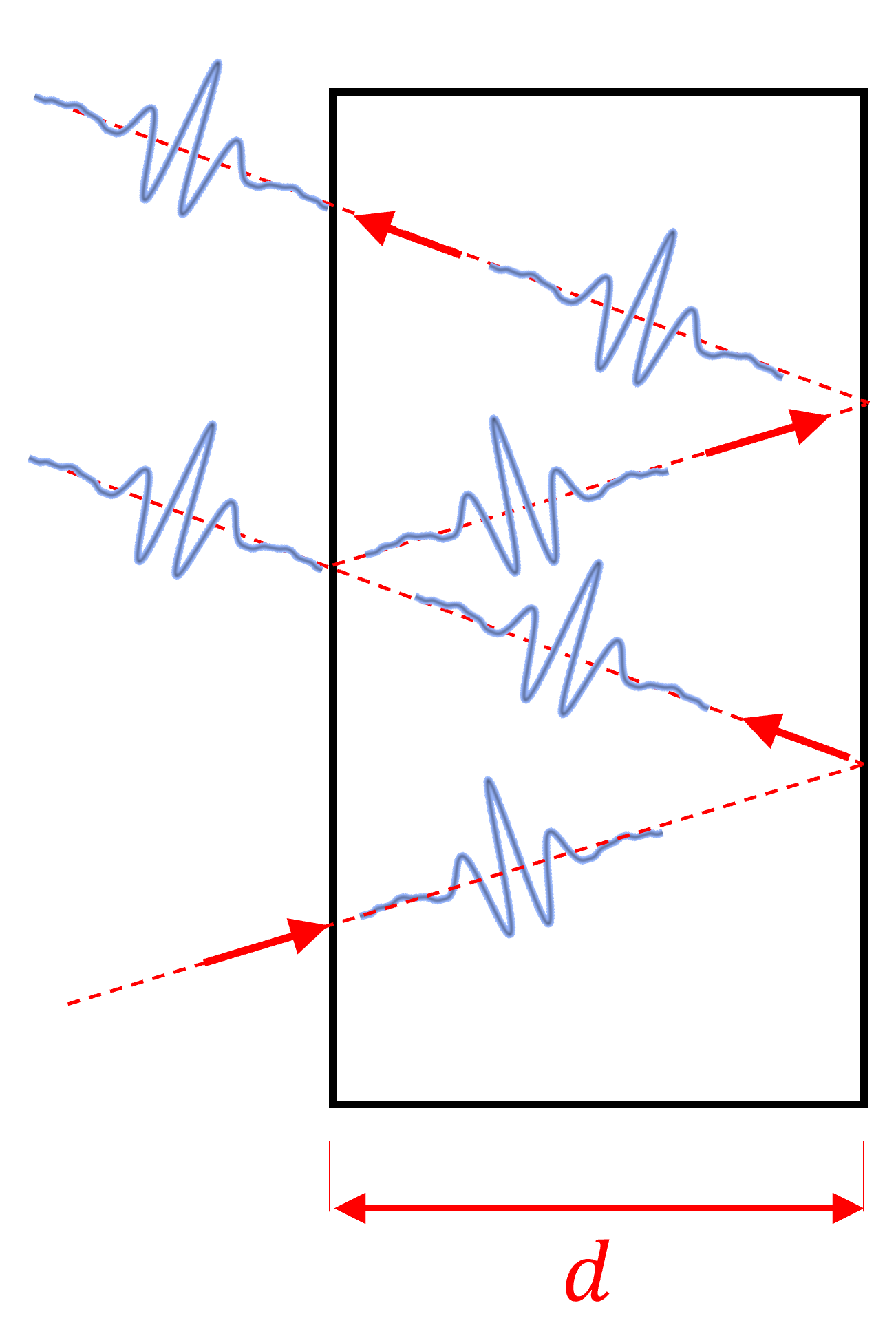
En general, para una longitud características $d$, la regla es:

Si $d > l_c$ el transporte de luz es incoherente . En este régimen, podemos ignorar las propiedades oscilatorias de la luz, y analizar el problema como el transporte de pequeños paquetes de onda, o simplemente como partículas.
Si $d < l_c$, el transporte de luz es coherente. En este régimen debemos considerar las propiedades oscilatorias a partir de las Ecuaciones de Maxwell.

Así, los coeficientes de Fresnel para una película delgada solo son aplicables si $d < l_c$.

Los coeficientes de Fresnel para una interface, en cambio, siempre son válidos debido a que consideran una interface infinitamente delgada.

Refracción y reflexión de una onda incoherente a través de una interfaz

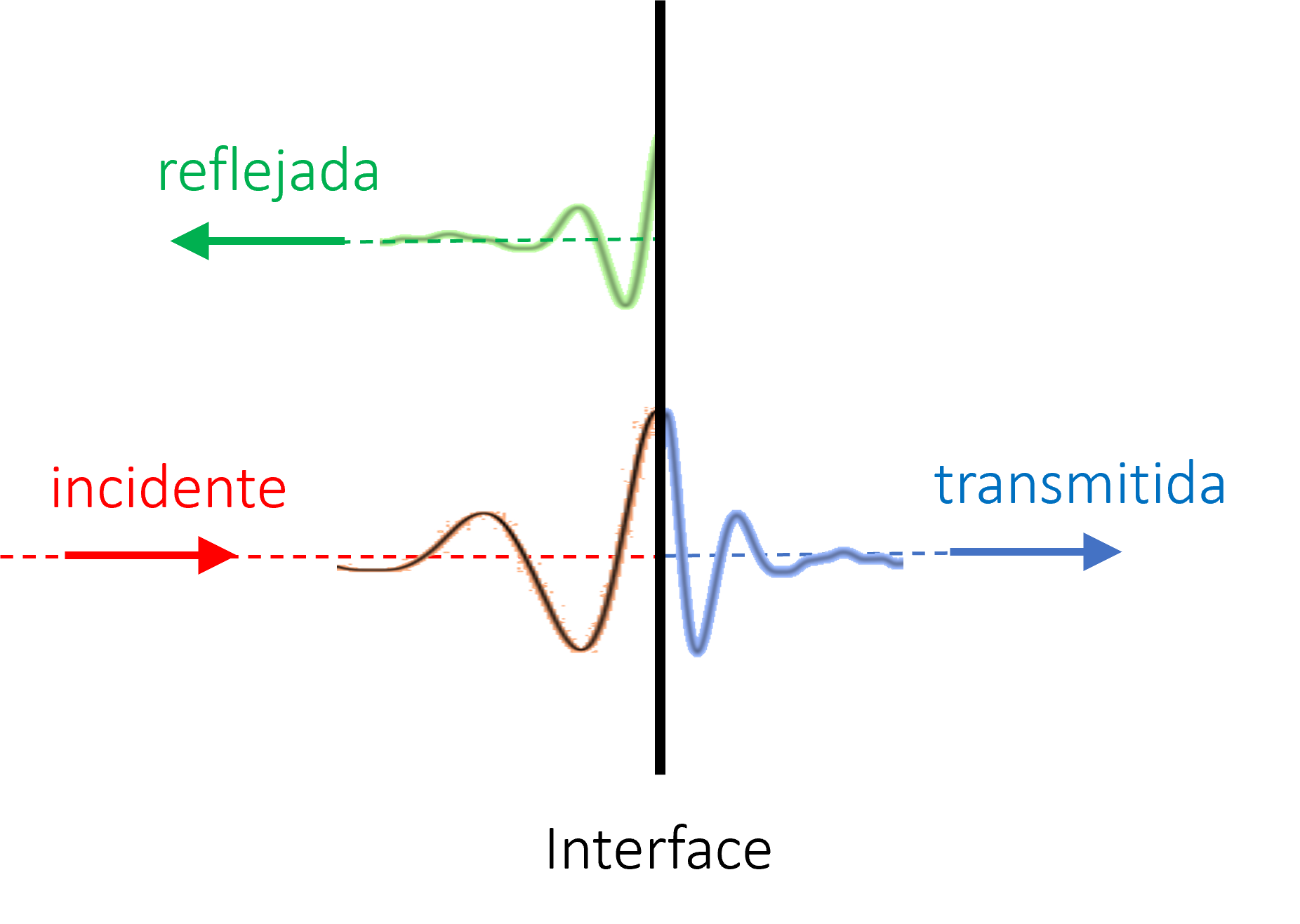
En medios particulados, los fenómenos de interferencia pueden ocurrir si las partículas están suficientemente cerca y tienen tamaños similares. Llamamos a esto scattering coherente

Fenómeno de interferencia en scattering

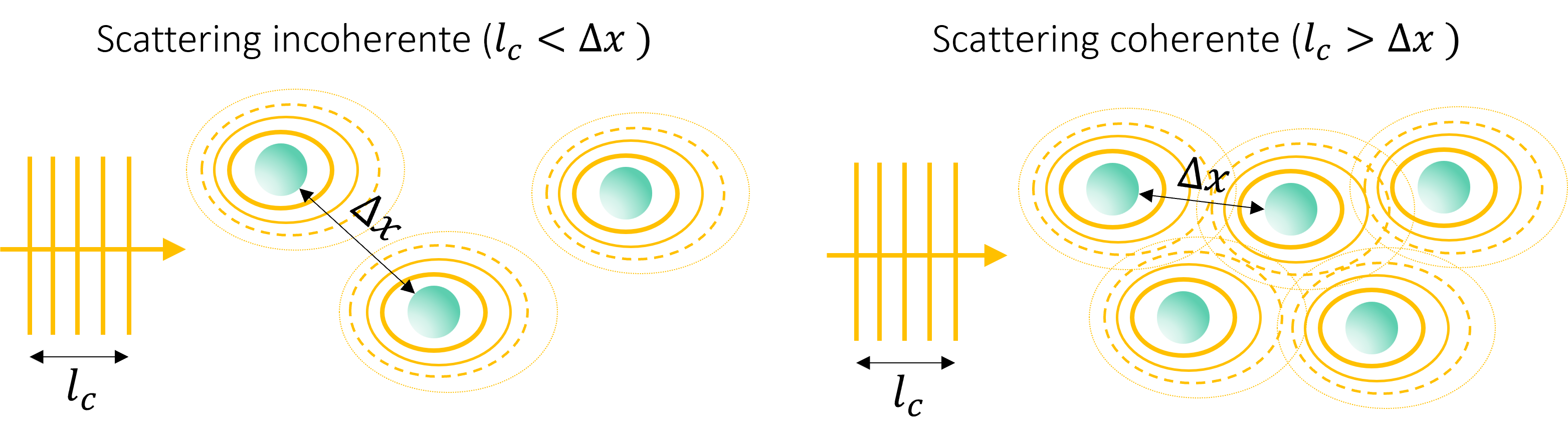
El fenómeno de scattering coherente da lugar a los denominados colores estructurales presentes en las alas de las aves y mariposas (mas info acá)

Colores estructurales en alas de aves

Fuente: Hwang, V. et al. PNAS 118 (4) e2015551118 (2020)

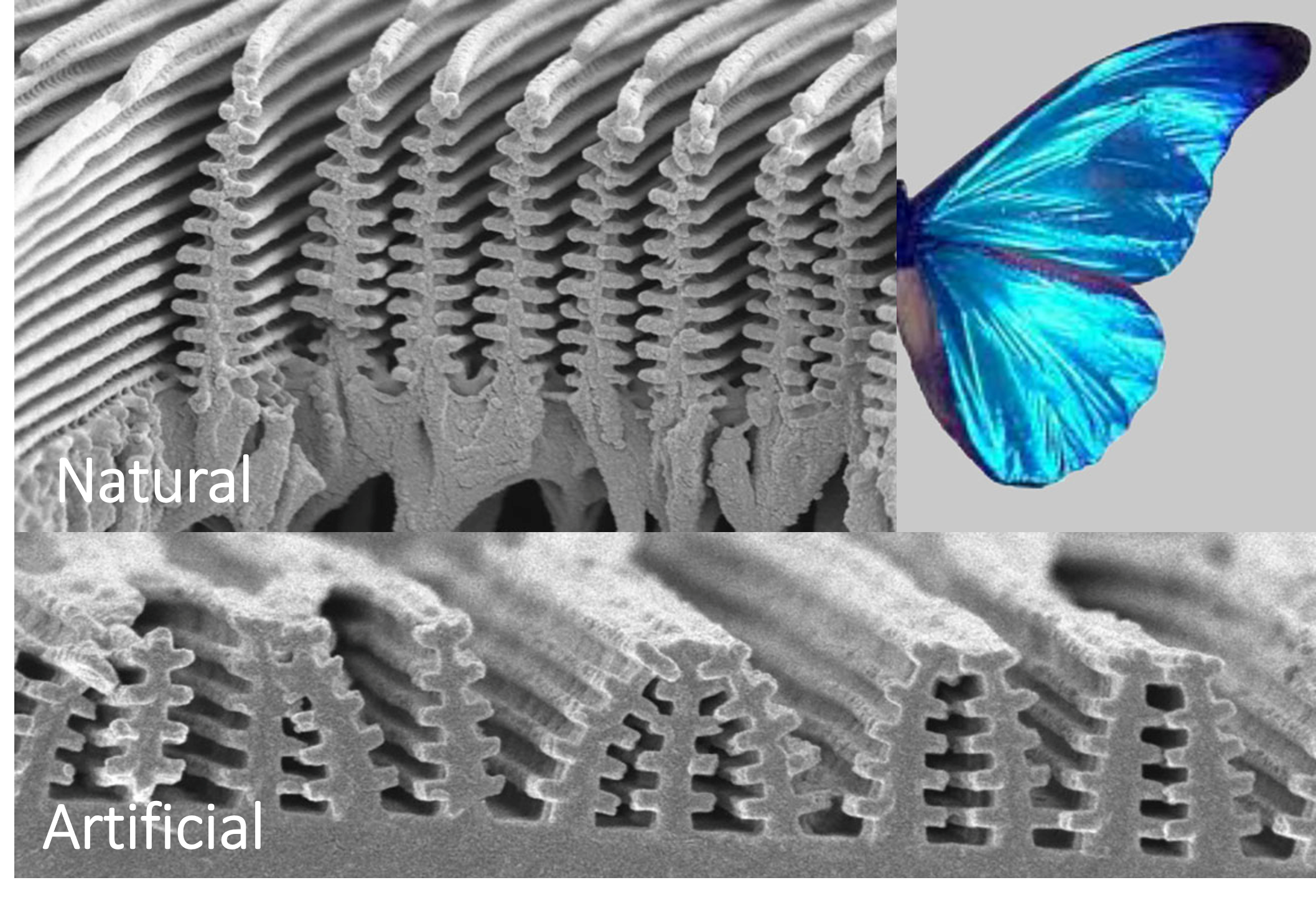
../_images/structural_colors_buterflies.png

Colores estructurales en alas de mariposa

Fuente: Tippets C. A. et al. J. Opt. 18 (2016) 065105

5.3. Teoría de transferencia radiativa#

Si el transporte de luz es incoherente, podemos ignorar las propiedades oscilatorias de la luz y analizar el fenómeno óptico como un el transporte de paquetes de ondas a través de un volumen de control. En otras palabras, al ignorar los efectos oscilatorios, solo analizamos la propagación de la intensidad de la luz en un medio

5.3.1. Intensidad específica#

Definimos como radiancia espectral o intensidad específica, $I_\lambda$, al flujo de energía por ángulo sólido diferencial, $d\Omega$, para una longitud de onda $\lambda$.

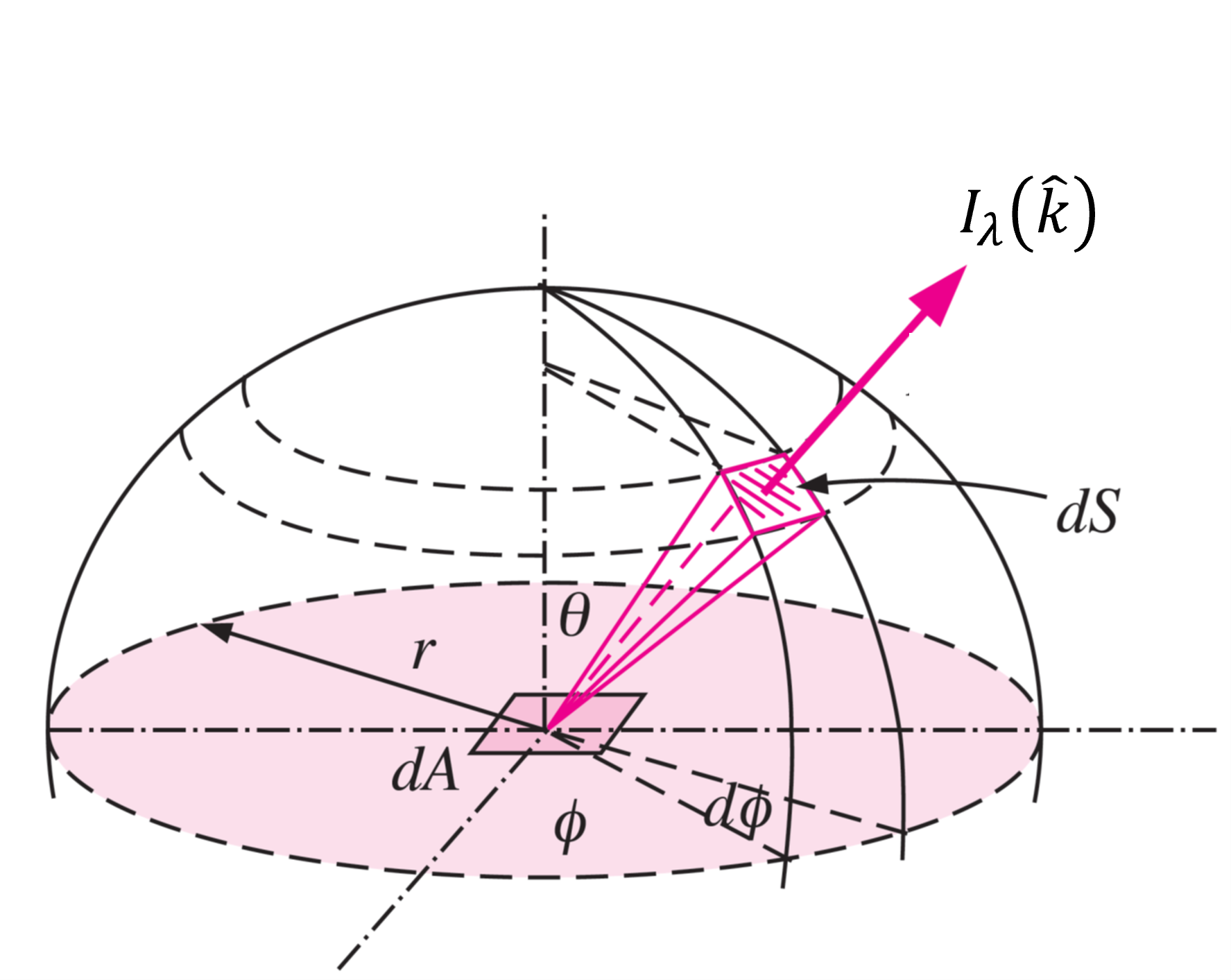
El ángulo sólido define el tamaño relativo del área $S$ para un observador en $P$ a una distancia $r$.

El diferencial está definido por $d\Omega = \sin\theta d\theta d\phi$

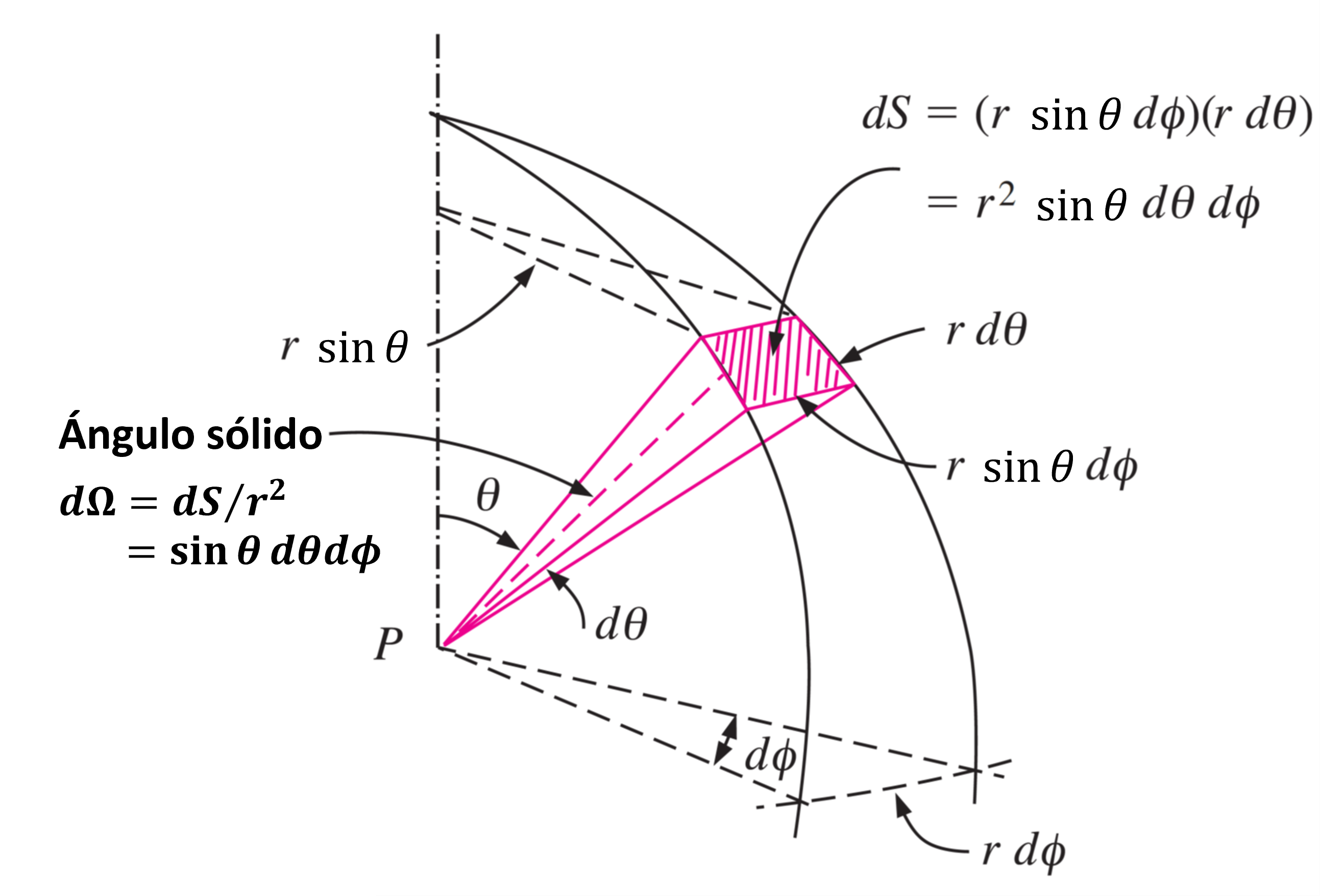
Es importante aclarar que los conceptos intensidad específica y vector de Poynting $\langle\vec{S}\rangle$, son equivalentes: $I_\lambda(\hat{k})$ es un término utilizado en radiometría para definir el flujo de energía por unidad de ángulo sólido, mientras que $\langle\vec{S}\rangle$ es un término utilizado en óptica para describir el flujo de energía en dirección $\hat{k}$.

5.3.2. Ecuación de transferencia radiativa#

La ecuación de transferencia radiativa (RTE por sus siglas en ingles), es una ecuación de transporte que describe el cambio de la radiancia espectral, $I_\lambda(\vec{r},\hat{k})$, en función de la posición posición $\vec{r}$ y dirección $\hat{k}$, producida por los efectos de scattering y absorción, este último, por las partículas dentro de un material, como por el material mismo.

En su forma más general, para un problema estacionario:

(5.1)#\[\begin{equation} \hat{k}\cdot\nabla_r I_\lambda(\vec{r},\hat{k}) = - \left[\frac{f_v}{V_p}C_\mathrm{ext} + 2\kappa k_0\right]I_\lambda(\vec{r},\hat{k}) + \frac{f_v}{V_p}\int_{4\pi} P_\mathrm{sca}\left(\hat{k},\hat{k}'\right) I_\lambda(\vec{r},\hat{k}') d\hat{k}' \end{equation}\]

donde $f_v$ y $V_p$ son, respectivamente la fracción de volúmen y el volúmen de las partículas en el medio, y $P_\mathrm{sca}(\hat{k},\hat{k}')$ es la función de fase.

Notar que consideramos el caso más generalizado de la función de fase, que depende tanto de la dirección de la radiación incidente $\hat{k}$ como de la dirección del scattering $\hat{k}'$. Ambas definidas por ángulo sólido

En el caso de una esfera, la dirección de la onda incidente es irrelevante (simetría esférica) y la función de fase depende del ángulo $\theta$ formado entre la onda incidente $\hat{k}$ y la de scattering $\hat{k}'$. Como vimos en la unidad anterior.

Con esto en mente, ahora podemos discutir el significado de los términos en la RTE:

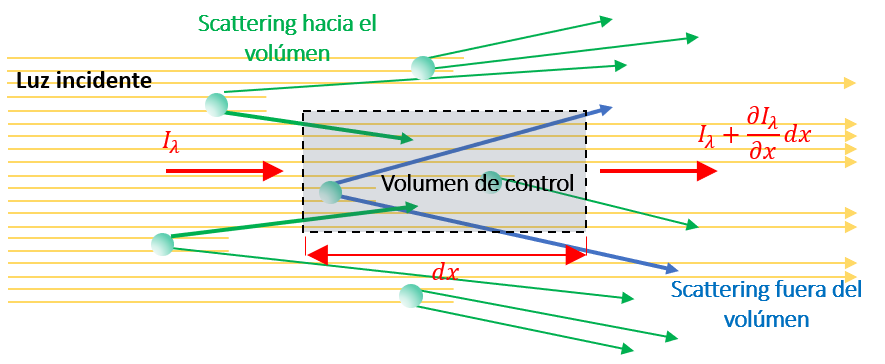
../_images/radiative_transfer_scketch.png

El primer término representa el cambio de $I_\lambda(\vec{r},\hat{k})$ a través volumen diferencial. Por ejemplo, en el caso unidimencional en dirección $\hat{k} = \hat{x}$, tenemos:

\[\begin{equation*} \hat{x}\cdot\nabla_r I_\lambda(\vec{r},\hat{k}) = \frac{\partial}{\partial x}I_\lambda(\vec{r},\hat{k}) \end{equation*}\]

El segundo término representa la pérdida de energía radiativa, por extinción $\left(\frac{f_v}{V_p}C_\mathrm{ext}\right)$ y absorción en el material material ($2\kappa k_0$), respectivamente. Recordemos que la extinción representa la energía absorbida por las partículas + la energía de scattering en direcciónes distintas a $\hat{k}$, es decir $C_\mathrm{ext}= C_\mathrm{abs} + C_\mathrm{sca}$.

El tercer término representa la ganancia de energía radiativa produco del scattering inducido por radiación incidente en dirección $\hat{k}'$. Este término representa el fenómeno de scattering múltiple.

5.4. Soluciones de la RTE#

La ecuación de transferencia radiativa permite explicar de forma fenomenológica el transporte de radiación en un medio particulado. Debido a su complejidad, existen pocas soluciones analíticas. En esta sección describiremos las tres más conocidas.

5.4.1. Película de material sin partículas (Reflectividad y Transmisividad incoherente)#

En el caso de un medio sin partículas solo debemos considerar el primer término del lado derecho de la RTE.

Considerando que el espesor del material, $t_\mathrm{film}$, el índice de refracción, $N = n + \kappa$, y que las regiones sobre y bajo el material tienen índice de refracción $N_0$, la solución está dada por las siguientes relaciones de reflectividad y tranmisividad para luz incoherente:

(5.2)#\[\begin{align} R_\mathrm{incoh}&= R_0 + \frac{T_0^2R_0e^{-4\kappa k_0 t_\mathrm{film}}}{1 - R_0^2e^{-4\kappa k_0 t_\mathrm{film}}} \\[10pt] T_\mathrm{incoh} &= \frac{T_0^2e^{-4\kappa k_0 t_\mathrm{film}}}{1 - R_0^2e^{-4\kappa k_0 t_\mathrm{film}}} \end{align}\]

donde $R_0$ y $T_0$ corresponden, respectivamente, a la reflectividad y transmisividad en la interface $N_0 / N_1$

En el siguiente ejemplo, utilizamos la función incoh_multilayer de la libreria empylib.waveoptics. Esta función es más general que la ecuación anterior y permite determinar $R_\mathrm{incoh}$ y $T_\mathrm{incoh}$ para arreglos multicapas.

En este caso, evaluaremos una película de sílice de espesor $1~\mu\mathrm{m}$, sobre un sustrato con íncide de refracción $N_\mathrm{back} = 4.3$, y con aire en la superficie $N_\mathrm{front} = 1.0$. El espectro de longitudes de onda $\lambda\in[0.3,0.8]~\mu\mathrm{m}$ y el ángulo de incidencia $\theta_i = 30°$. Para comparar, determinaremos $R$ y $T$ para el caso de luz coherente.

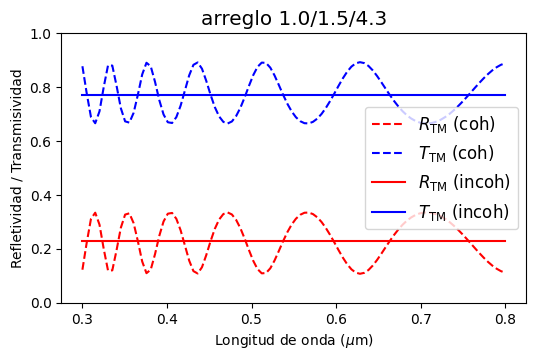
../_images/4dc26402488434fcdcb13b70cec6a35e543a80fe5f212c254026dd8497c4366e.png

En la figura, para el caso de luz coherente, notamos oscilaciones en $R$ y $T$ producto de los fenómenos de interferencia. En el caso de luz incoherente, el fenómeno de interferencia desaparace. $R$ y $T$ son constantes independiente de la longitud de onda.

5.4.2. Película de material con baja concentración de partículas (Ley de Beer-Lambert)#

Definimos el camino libre medio de scattering, como $\Lambda_\mathrm{sca} = \left(f_v C_\mathrm{sca}/V_p\right)^{-1}$. Este parametro representa la distancia promedio que recorre la luz entre eventos de scattering.

Si $\Lambda_\mathrm{sca}$ es mayor que el espesor del material, $t_\mathrm{film}$, la probabilidad de que ocurran más de un evento scattering es despreciable, y decimos que el scattering es de primer orden. En este caso, el tercer término del lado derecho de la RTE es despreciable y la radiación solo pierde energía por absorción del material o extinción inducida por las partículas.

La solución a esta ecuación se conoce como la ley de Beer-Lambert. Mediante esta aproximación podemos deducir las componentes total y especular de la transmitancia:

(5.3)#\[\begin{equation} T_\mathrm{tot} = T_0 e^{-f_v\frac{C_\mathrm{abs}}{V_p}t_\mathrm{film}}\quad\quad\mathrm{and}\quad\quad T_\mathrm{spec} = T_0 e^{-f_v\frac{C_\mathrm{ext}}{V_p}t_\mathrm{film}} \end{equation}\]

donde, $T_0$ es la transmisividad incoherente del material sin incrustaciones.

Transporte de luz en un medio con scattering de primer orden

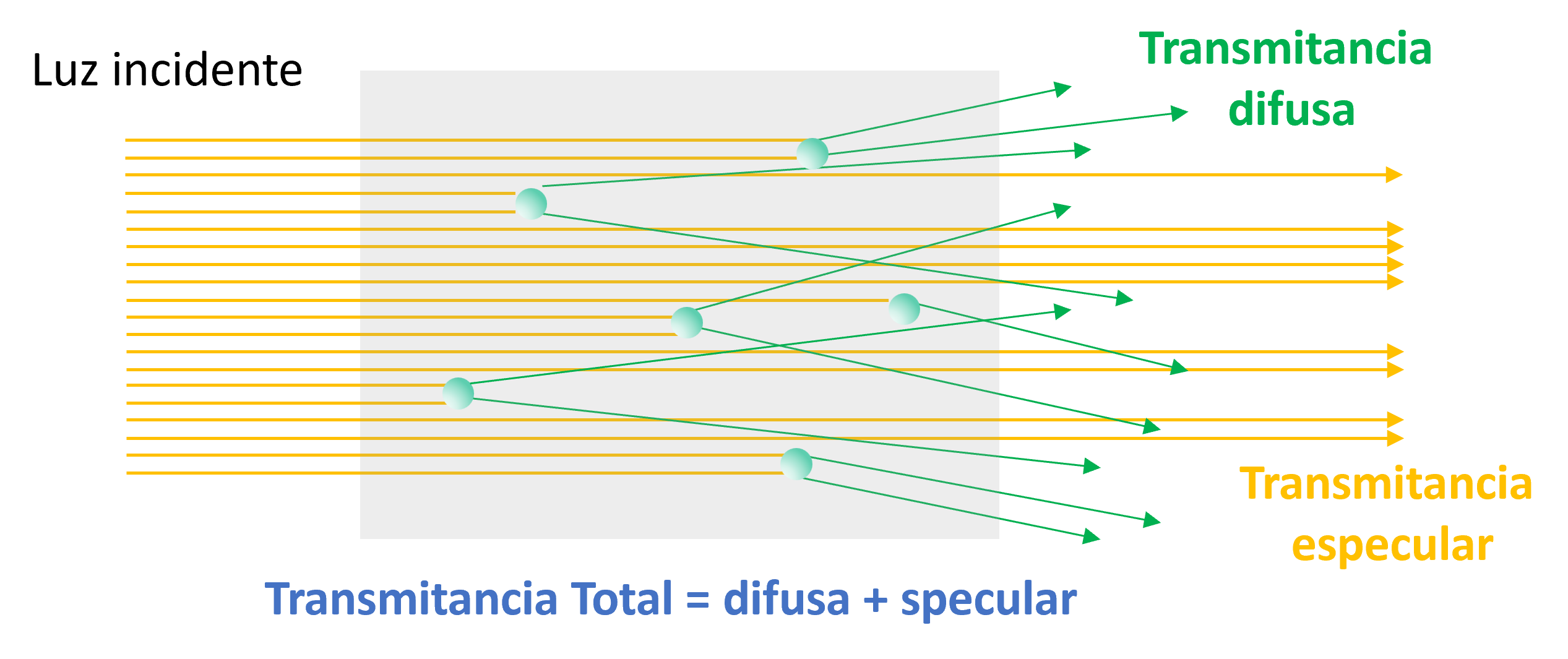
Podemos utilizar la ley de Beer-Lambert para analizar, de forma aproximada, el efecto del color del cielo durante el día y en la tarde.

El color del cielo está dado por la componente difusa. Así calculamos $T_\mathrm{dif} = T_\mathrm{tot} - T_\mathrm{spec}$.

Consideremos una atmosfera compuesta de aire ($N_h = 1.0$) y una pequeña concentración ($f_v = 1\times 10^{-6}~\%$) de partículas de 10 nm de diámetro e índice de refracción $N_p = 1.5$. El espesor de la atmosfera es $t_\mathrm{atm} = 100~\mathrm{km}$

5.4.3. Pelicula de material particulado (simulaciones de transferencia radiativa)#

Este caso corresponde a materiales con $\Lambda_\mathrm{sca} < t_\mathrm{film}$. En este caso los eventos de scattering se producen más de una vez, y decimos que estámos en un régimen de scattering múltiple. Como resultado, los tres términos de la RTE son relevantes y debemos resolver la ecuación mediante simulación computacional.

Transporte de luz en un medio con scattering múltiple

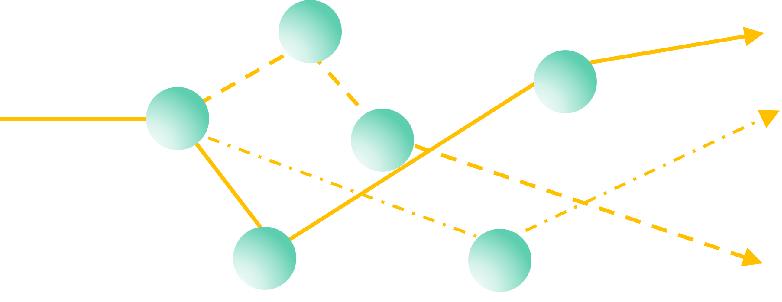
Analicemos la copa de Licurgo, considerando un material de sílice de espesor $t_\mathrm{film} = 5~\mathrm{mm}$ con incrustaciones de partículas de plata de forma esférica.

Evaluaremos los colores de este material en transmisión y reflexión para luz incidente normal a la superficie en función de la concentración y el diámetro de las partículas. Utilizamos la función adm_sphere de la librería empylib.rad_transfer

Show code cell source Hide code cell source

import empylib.rad_transfer as rt
import empylib.nklib as nk
import empylib.miescattering as mie
import numpy as np
import matplotlib.pyplot as plt

lam2 = np.linspace(0.3,1.0,100) # espectro de longitudes de onda en micrometros
Nlayers = (1.0,1.5,1.0)         # indice de refracción superior, intermedio e inferior
Np = nk.silver(lam2)            # Índice de refracción de las partículas
cs.interp_internals(lam2)

def plot_glass_silver(fv,D):
    # parámetros de entrada
    
    theta = np.radians(0)       # 0 grados en radianes
    tfilm = 5                   # espesor en milímetros
    
    fv = fv*1E-7                # fracción de volúmen de las partículas
    D = D*1E-3                  # diámetro de las partículas
    
    qext, qsca = mie.scatter_efficiency(lam2,Nlayers[1],Np,D)[:2]
    qabs = qext - qsca
    Ttot, Rtot = rt.adm_sphere(lam2,tfilm,Nlayers,fv,D,Np)[:2]

    fig, ax = plt.subplots(1,3)
    fig.set_size_inches(12, 3)
    plt.rcParams['font.size'] = '10'
    
    ax[0].plot(lam2,qsca,'-r',label='$C_\mathrm{sca} A_c$')
    ax[0].plot(lam2,qabs,'-b',label='$C_\mathrm{abs} A_c$')
    ax[0].set_xlabel('Longitud de onda ($\mu$m)')
    ax[0].set_ylabel('Eficiencia transversal')
    ax[0].set_title('Partícula de plata (D=%.0f nm)' % (D*1E3))
    ax[0].legend()
    ax[0].set_ylim(0,10)
    
    ax[1].plot(lam2,Rtot,'-r',label = 'Rtot')
    ax[1].plot(lam2,Ttot,'-b',label = 'Ttot')
    ax[1].set_xlabel('Longitud de onda ($\mu$m)')
    ax[1].set_ylabel('Transmisividad')
    ax[1].set_title(r'Sílice con plata (fv = %.3e %%)' % (fv*100) )
    ax[1].legend()
    ax[1].set_ylim(0,1)

    Dcircle = 0.20
    html_rgb = cs.spec_to_rgb(Ttot*AM15(lam2), out_fmt='html')
    Circle = plt.Circle((0, 0), Dcircle, color=html_rgb)
    ax[2].add_patch(Circle)
    ax[2].annotate('Luz Transmitida', xy=(0, 0), va='center', ha='center')

    html_rgb = cs.spec_to_rgb(Rtot*AM15(lam2), out_fmt='html')
    Circle = plt.Circle((Dcircle*1.2*2, 0), Dcircle, color=html_rgb)
    ax[2].add_patch(Circle)
    ax[2].annotate('Luz Reflejada', xy=(Dcircle*1.2*2, 0), va='center', ha='center')

    ax[2].set_aspect('equal')
    ax[2].set_xlim(-Dcircle*1.2,Dcircle*1.2*3)
    ax[2].set_ylim(-Dcircle*1.2,Dcircle*1.2)
    ax[2].set_xticks([])
    ax[2].set_yticks([])
    ax[2].set_facecolor('k')
    plt.subplots_adjust(wspace=0.3)
    plt.show()

Cuando la concentración de partículas es densa, el medio se vuelve opaco. Este régimen se denomina scattering difuso y permite explicar, entre otras cosas, el color de las nubes o la pintura blanca

Transporte de luz en un medio con scattering difuso

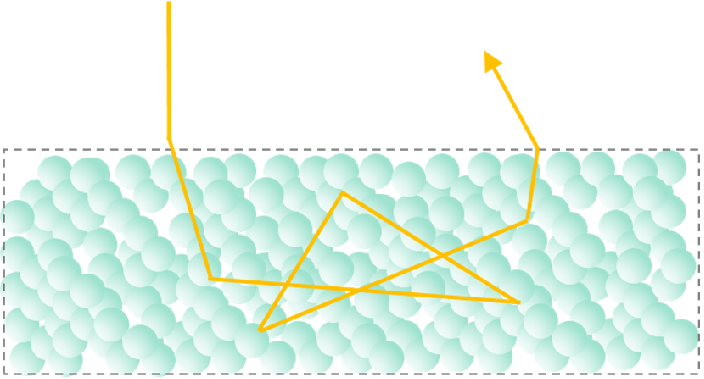
Un ejemplo interesante corresponde a la leche. En términos simples, la leche es una emulsión formada por pequeñas partículas de grasa dispersas en un medio acuoso.

Imagen de microscópio (40x) de leche orgánica. Las burbujas verdes corresponden al aceite en suspención en agua.

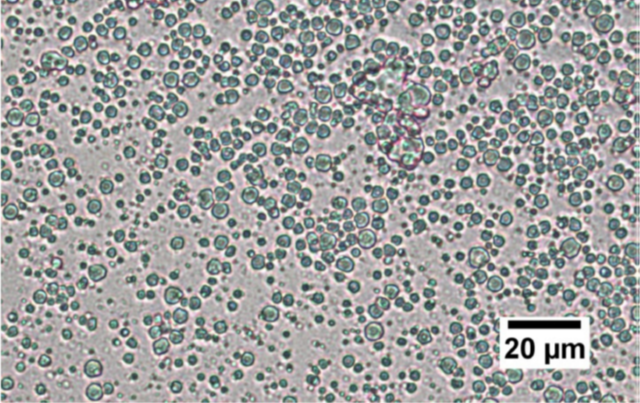
Fuente: Braun K., Hanewald A. and Vilgis T. Foods 8(10): 483(2019)

La luz es dispersada múltiples veces debido a la alta concentración de estas partículas de grasa. El resultado, la luz es totalmente reflejada (para todas las longitudes de onda), explicando el colr blanco de la leche.

Como aproximación, consideremos un medio de espesor $1$ cm, compuesto por agua $N_h = 1.3$ y pequeñas partículas esféricas de aceite $N_p = 1.5$. La emulsión considera un 60% de partículas de aceite por volumen.

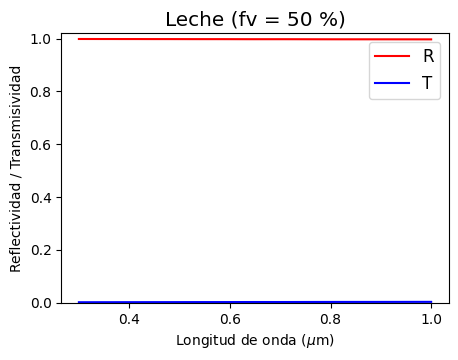
../_images/98a12e62c83754a533e815ba9c097c2b18a91ad77404cd3cb6b5bd6a003dcb9d.png

Como vemos la alta concentración de partículas hace que la refletividad y transmisividad se vuelvan casi uniformes para todas las longitudes de onda. El espectro, así, toma un color blanco frente a una fuente de luz blanca.

5.5. Referencias#

Chen G. Chapter 5 - Energy Transfer by Waves in Nanoscale energy transport and conversion, 1st Ed, Oxford University Press, 2005