3. Propiedades ópticas de los materiales

3.1. Fundamentos del movimiento oscilatorio

3.1.1. Frecuencia natural de un sistema vibratorio

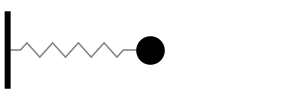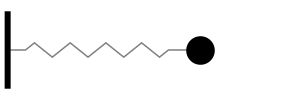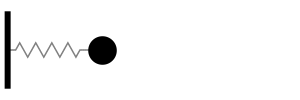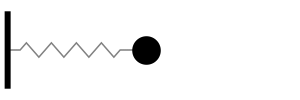
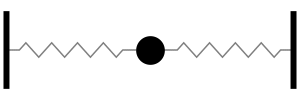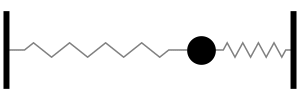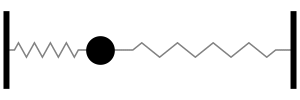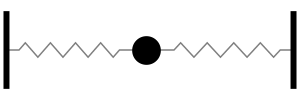
Analicemos el caso simplificado de un sistema masa resorte

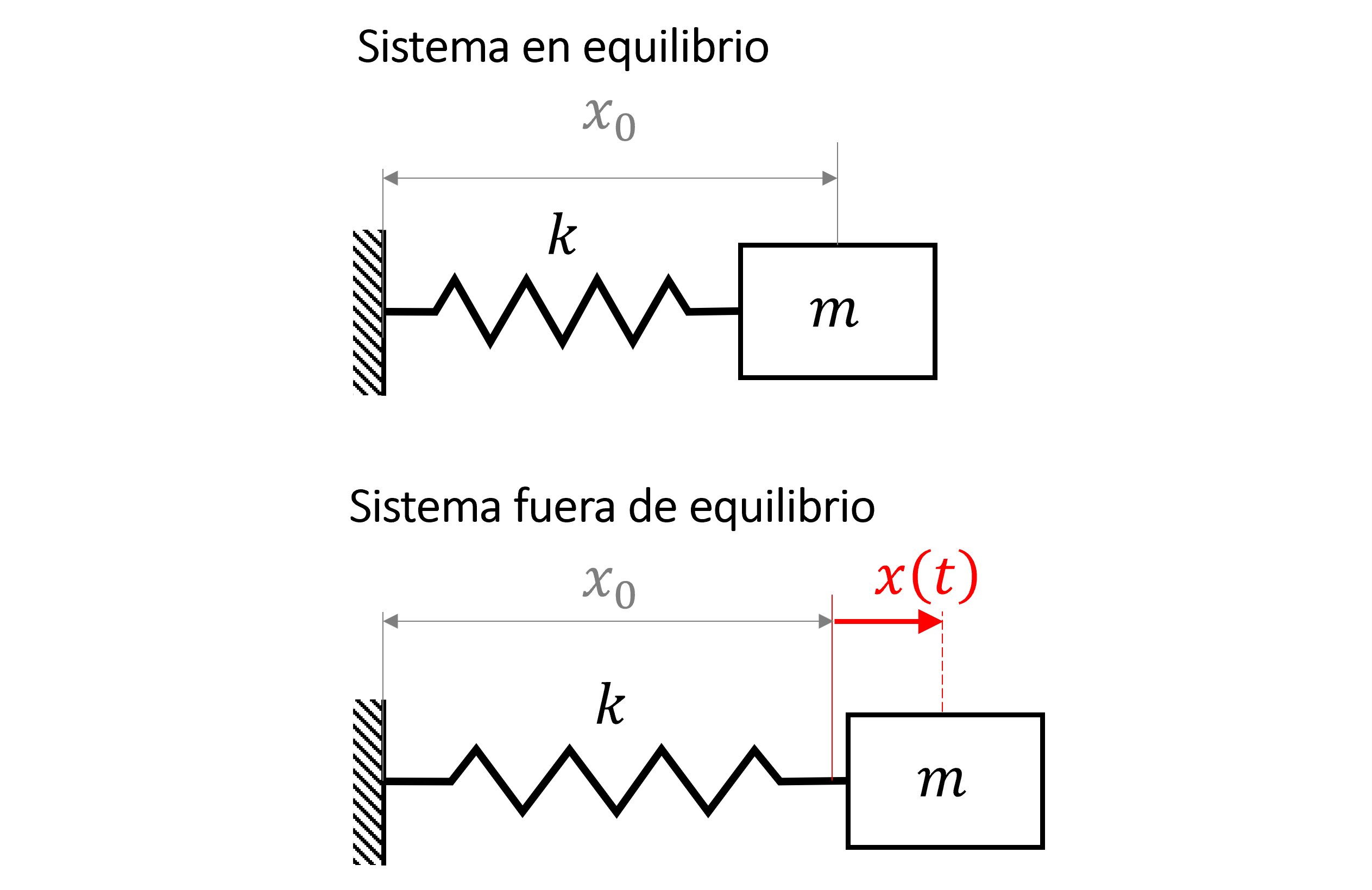
donde, \(k\) es la constante de rigidez del resorte, y \(m\) es la masa.

El resorte ejerce una fuerza de restauración, \(F_\mathrm{res} = kx\), que actúa en sentido contrario al desplazamiento de la masa.

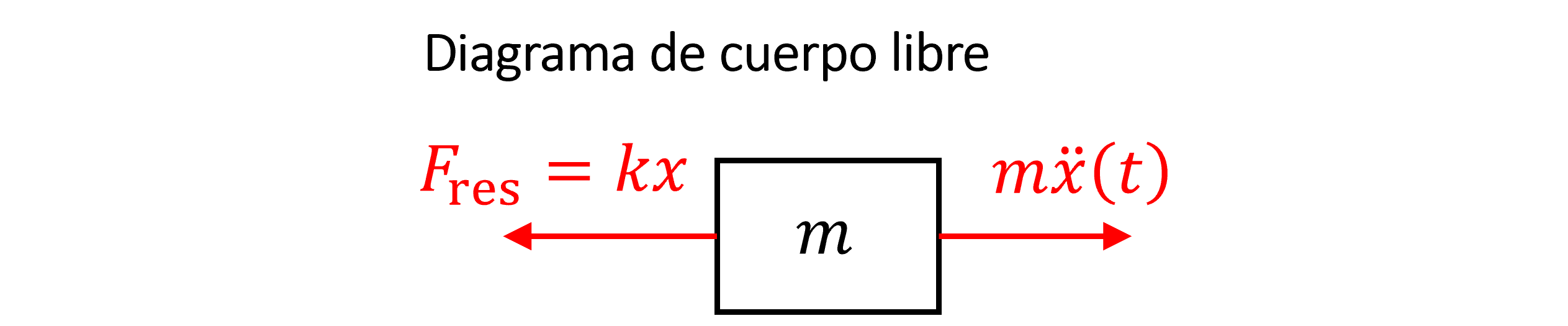
Mediante un equilibrio de fuerzas, deducimos la ecuación gobernante del sistema masa-resorte:

\[\begin{equation*} \ddot{x} + \omega_n^2 x = 0 \end{equation*}\]

donde \(\omega_n = \sqrt{k/m}\), es la frecuencia natural del sistema

La frecuencia natural de un sistema vibratorio representa la frecuencia de oscilación del sistema en ausencia de amortiguación y fuerzas externas.

Es una firma espectral que solo se puede cambiar ajustando la masa \(m\) o la constante de rigidez del sistema \(k\).

Esto significa que, ante cualquier perturbación del sistema en equilibrio, el sistema oscilará en su frecuencia natural \(\omega_n\).

Sistema con 1 grado de libertad (Fuente: Daniel A. Russell)

Cada sistema tiene una frecuencia natural, que puede estar definida por distintos parámetros. Sin embargo, la característica más importante, es la presencia de una fuerza de restauración opuesta al movimiento del cuerpo.

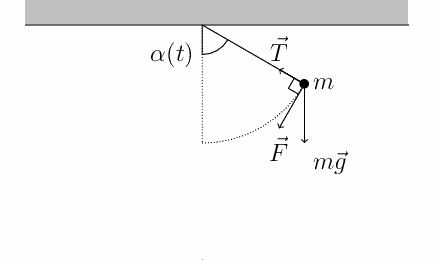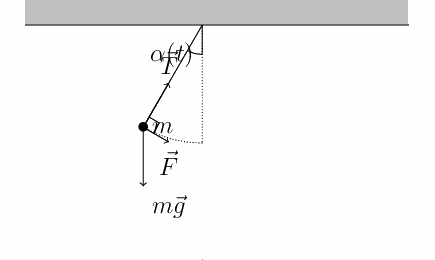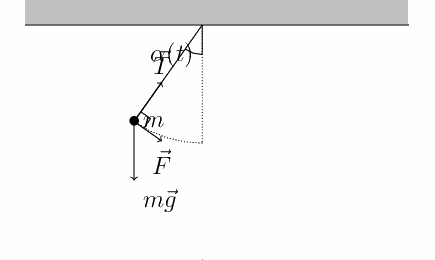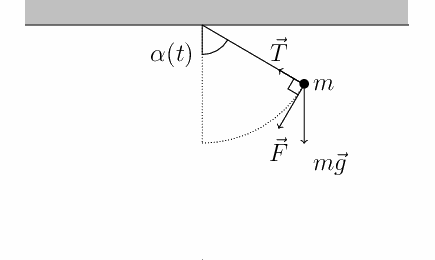
Por ejemplo, en un péndulo, la fuerza de restauración corresponde a la componente de la fuerza de gravedad que actúa en sentido contrario a la aceleración del cuerpo.

3.1.2. Vibración forzada amortiguada con un grado de libertad

La frecuencia natural cobra relevancia cuando analizamos vibraciones forzadas.

Consideremos, por ejemplo, un sistema masa-resorte amortiguado, donde \(c\) es la constante de amortiguación. El sistema es excitado por una fuerza externa oscilatoria de la forma \(F(t) = F_0 e^{i\omega t}\), donde \(F_0\) es una constante.

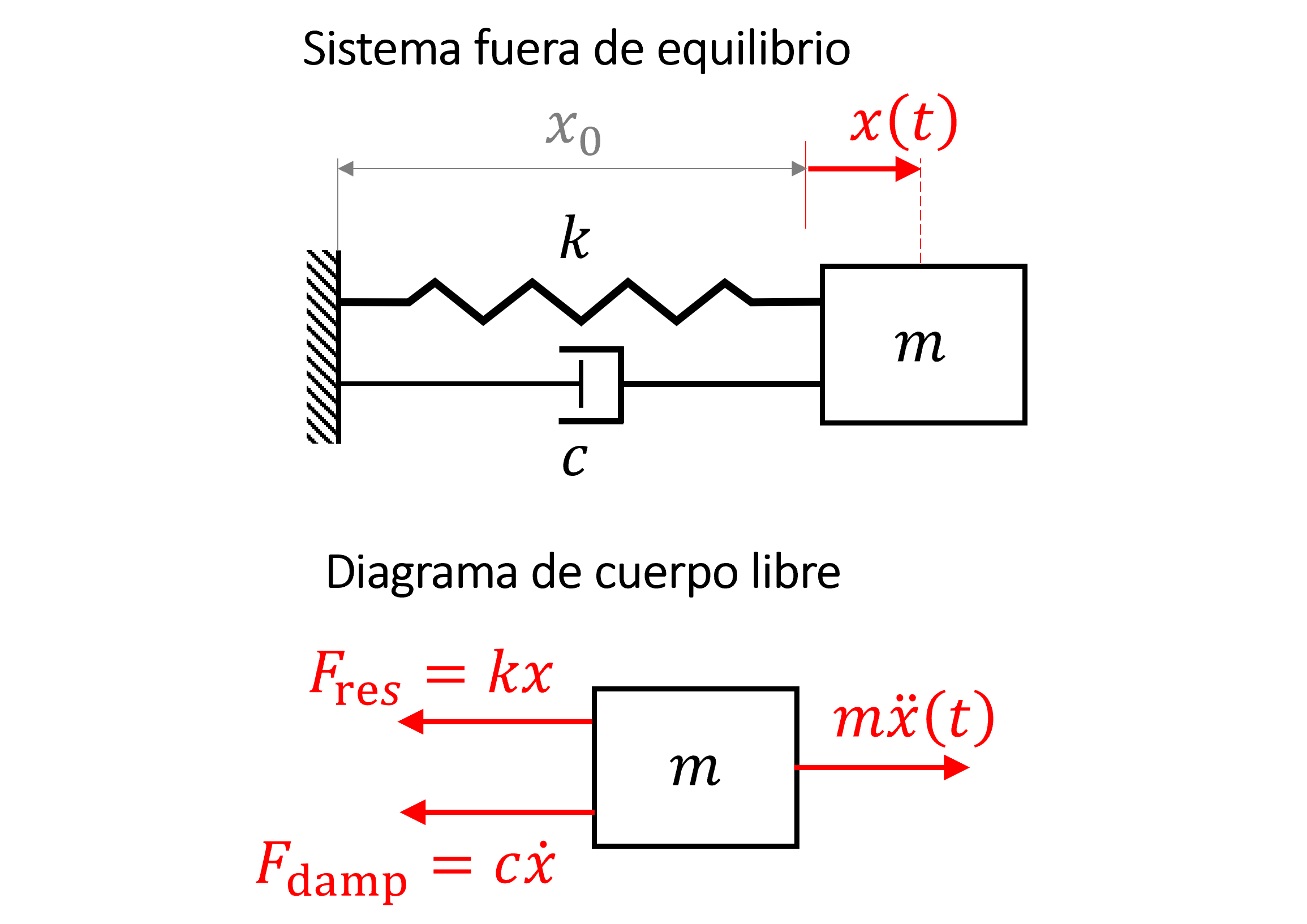
Ahora, la ecuación gobernante es:

\[\begin{equation*} \ddot{x} + \frac{c}{m}\dot{x} + \omega_n^2 x = \frac{F_0}{m} e^{- i\omega t}, \end{equation*}\]

La solución estacionaria es de la forma \(x = Ae^{-i\omega t}\):

\[\begin{equation*} x(t) = - \frac{F_0/m}{\omega^2 - \omega_n^2 + i\frac{c}{m} \omega}e^{- i\omega t} \end{equation*}\]

donde \(A = - \frac{F_0/m}{\omega^2 - \omega_n^2 + i\frac{c}{m} \omega}\) es la amplitud de la respuesta oscilatoria.

La ecuación indica que la amplitud de la respuesta depende principalmente, de la frecuencia de la fuerza externa \(\omega\).

Más aún, como vemos en esta herramienta interactiva de movimiento forzado amortiguado, cuando \(\omega \approx \omega_n\) la amplitud aumenta a un límite crítico.

Respuesta ante fuerza oscilatoria (Fuente: Daniel A. Russell)

En este caso decimos que el sistema está en resonancia.

La mejor forma de visualizar este fenómeno es analizando la amplitud en función de la frecuencia de la fuerza externa \(\omega\). En el gráfico a continuación mostramos el valor del módulo de la amplitud, \(|A|\) (izquierda) y la parte real e imaginaria de la amplitud (derecha).

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt

def x_amplitude(k,c):
    
    m = 1                                           # masa del cuerpo
    w = np.linspace(0,2,200)                       # rango de frecuencias
    F0 = 1                                          # Amplitud de la fuerza
    wn = np.sqrt(k/m)                               # frencuencia natural
    A  = lambda x: - F0/m/(x**2 - wn**2 + 1j*c/m*x) # amplitud de la respuesta
    
    # formateamos el lienzo para graficar
    fig, ax = plt.subplots(1,2)             # número de ejes en la figura
    fig.set_size_inches(10, 3)              # tamaño de la figura
    plt.rcParams['font.size'] = '12'        # tamaño de fuente
    
    # Ploteamos gráfico izquierdo
    ax[0].plot(w,np.absolute(A(w)),'k',label="$|A|$")     # módulo de la amplitud
    
    # marcar línea de frecuencia natural
    ax[0].axvline(x = wn, color='r', ls='--', lw='1.0')  
    ax[0].text(wn*1.01,np.absolute(A(wn)),'$\omega_n$', fontsize='12', color='r')
    
    # etiquetar valores de m y F0 en el gráfico
    x0, y0 = 0.1, 100
    ax[0].text(x0, y0,r'$m$ = %.0f kg'   % m , fontsize='10', color='k')
    ax[0].text(x0, y0*0.55,r'$F_0$ = %.0f N'% F0, fontsize='10', color='k')
    
    # Ploteamos gráfico derecho
    ax[1].plot(w,A(w).real,'b',label=r"$\mathrm{Re}(A)$") # parte real de la amplitud
    ax[1].plot(w,A(w).imag,'r',label=r"$\mathrm{Im}(A)$") # parte imaginaria de la amplitud
    
    for i in [0,1]:
        ax[i].set_xlabel('$\omega$ ')
        #ax[i].grid() 
        ax[i].set_xlim(0,2.0)
        ax[i].legend(frameon=False)
    ax[0].set_yscale('log')
    ax[0].set_ylim(0.1,200)
    ax[0].set_ylabel('Módulo de la amplitud')
    ax[1].set_ylabel('Amplitud')
    plt.subplots_adjust(wspace=0.3)
    plt.show()

Show code cell source Hide code cell source

from ipywidgets import interact

@interact( k=(0.3,2.0,0.1), 
           c=(0.02,0.2,0.01))
def g(k=1, c=0):
    return x_amplitude(k,c)

La frecuencia de resonancia es fundamental en el diseño de puentes, edificios, instrumentos acústicos y otras.

Un ejemplo emblemático es el colapso del puente Tacoma en 1940.

El puente se derrumbó debido al aleteo aeroelástico producido por los vientos, el cual coincidía con la frecuencia natural del puente

Otro ejemplo típico es el columpio

En este caso, la fuerza externa son las piernas. La resonancia se alcanza cuando estas se mueven en sincronía con la frecuencia natural del péndulo. El efecto de amortiguación en este caso, está dado por el arrastre del viento, fricción, etc.

3.1.3. Sistemas vibratorios con más de un grado de libertad

Un sistema vibratorio puede tener más de una frecuencia natural. El número de frecuencias naturales está directamente relacionado con el número de grados de libertad del sistema.

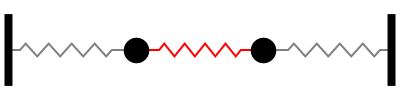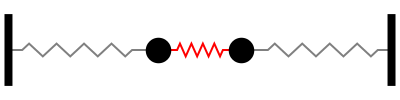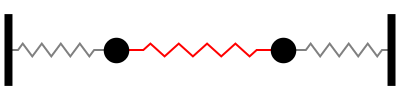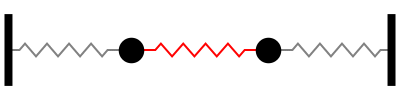
Sistema con 1 grado de libertad (aquí la frecuencia natural cambia a \(\omega_n = \sqrt{2k/m}\), debido a la presencia de 2 resortes)

modo	\(\omega_n\)
1	\(1.414\sqrt{k/m}\)

Sistema con 1 grado de libertad (Fuente: Daniel A. Russell)

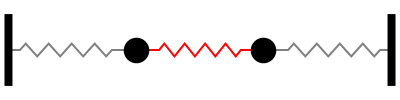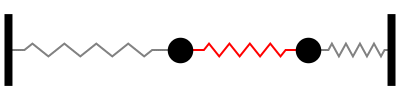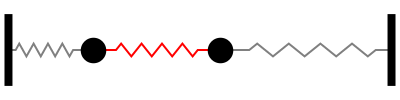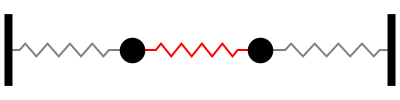
Sistema con 2 grados de libertad

modo	\(\omega_n\)
1	\(1.000\sqrt{k/m}\)
2	\(1.732\sqrt{k/m}\)

Sistema con 2 grados de libertad (Fuente: Daniel A. Russell)

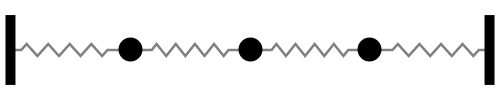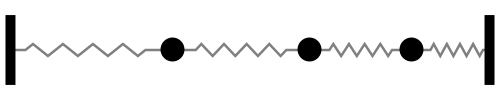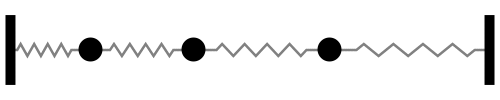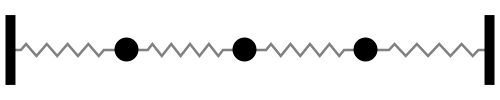
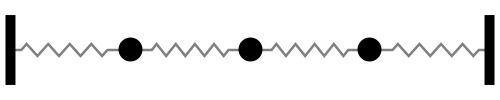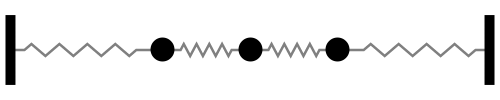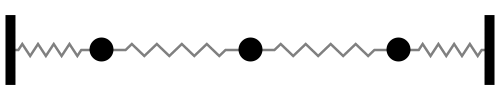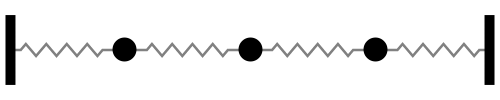
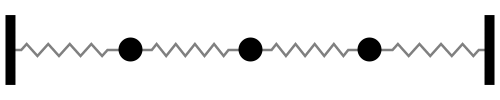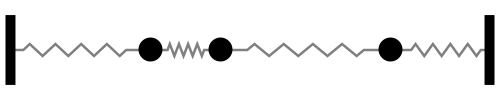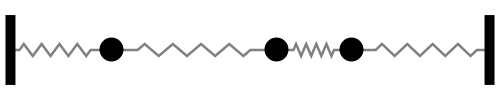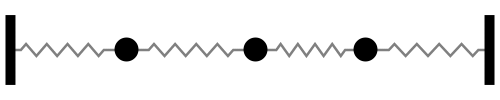
Sistema con 3 grados de libertad

modo	\(\omega_n\)
1	\(0.765\sqrt{k/m}\)
2	\(1.414\sqrt{k/m}\)
3	\(1.868\sqrt{k/m}\)

Sistema con 3 grados de libertad (Fuente: Daniel A. Russell)

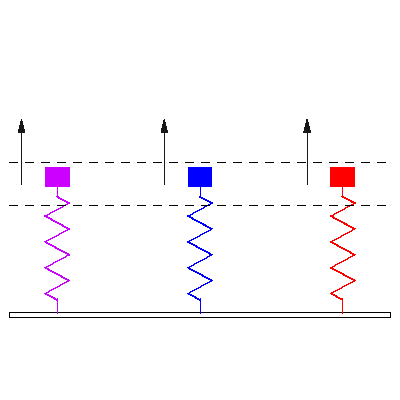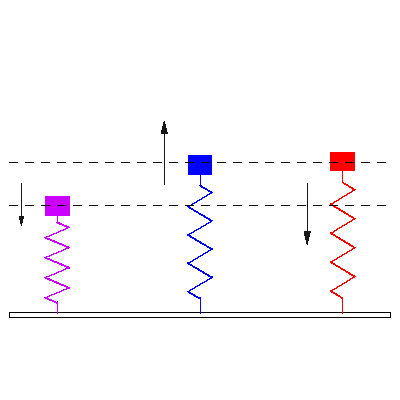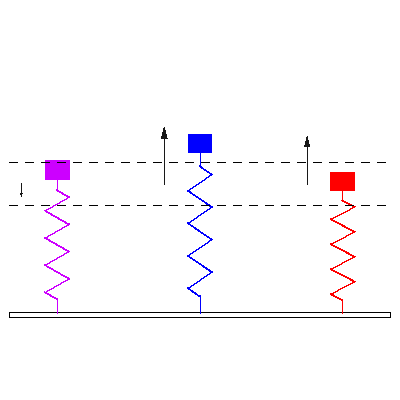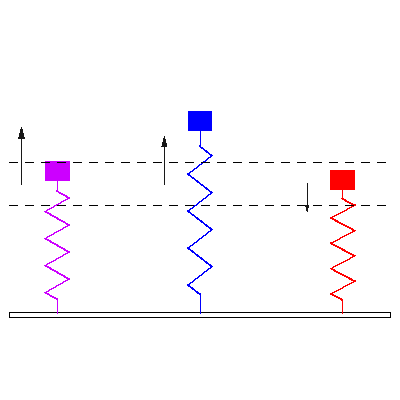
Notar la forma en que las frecuencias naturales se distribuye a medida que aumentamos los grados de libertad del sistema (Las flechas rojas indican la dirección de las masas asociada a cada modo de vibración):

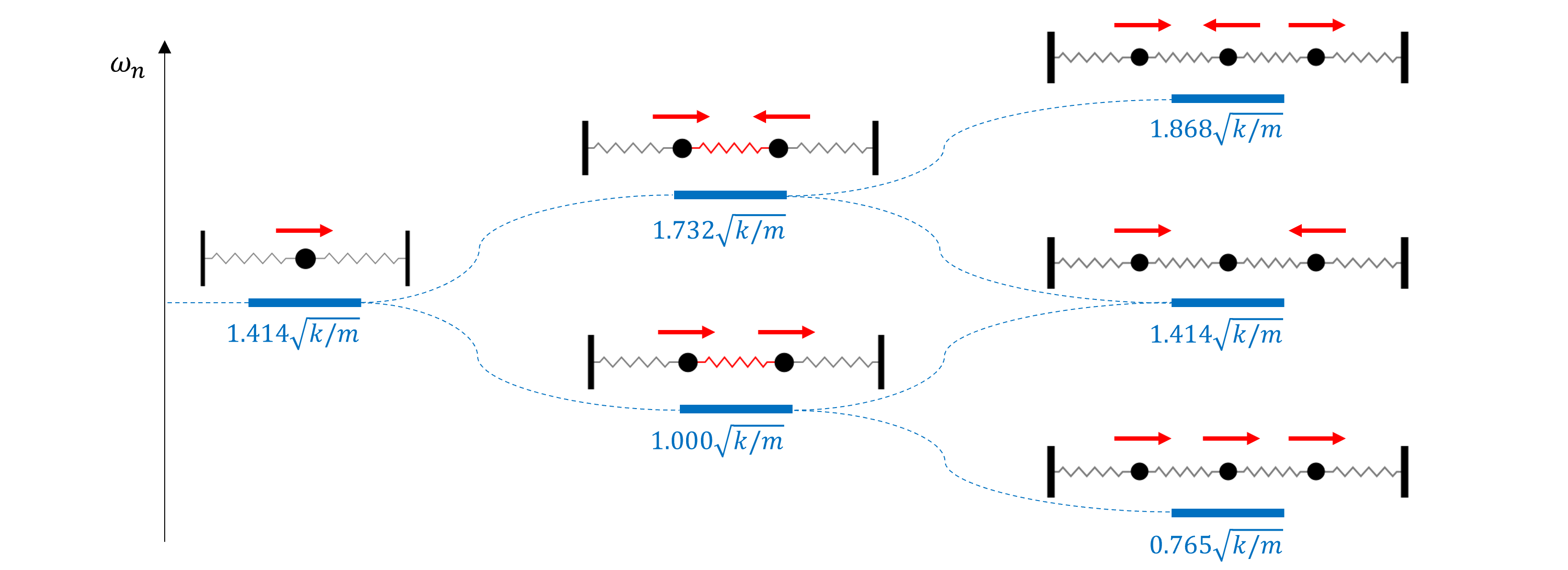
A diferencia de los sistemas con un grado de libertad, estos sistemas aclanzará la condición de resonancia cuando la fuerza oscilatoria externa cumpla dos condiciones:

• La frecuencia de oscilación (\(\omega\)) es igual a la frecuencia natural de uno de los modos

• La dirección es compatible con el movimiento de cada elemento en el sistema.

En otras palabras, tomando la figura anterior como referencia, la fuerza externa sobre cada masa debe tener la frecuencia y dirección indicada por las flechas rojas para activar la resonancia del sistema.

3.2. Interacción de luz con gases

Considerando la discusión anterior, nuestro objetivo es explicar la interacción de la luz con la materia y desarrollar un modelo matemático para la constante dieléctrica del material \(\varepsilon\) (o bien, el índice de refracción \(N\)).

El modelo para gases es el más simple. En este caso, cada molécula representa un sistema oscilatorio independiente, como veremos a continuación.

3.2.1. El oscilador armónico

Consideremos la molecula de agua.

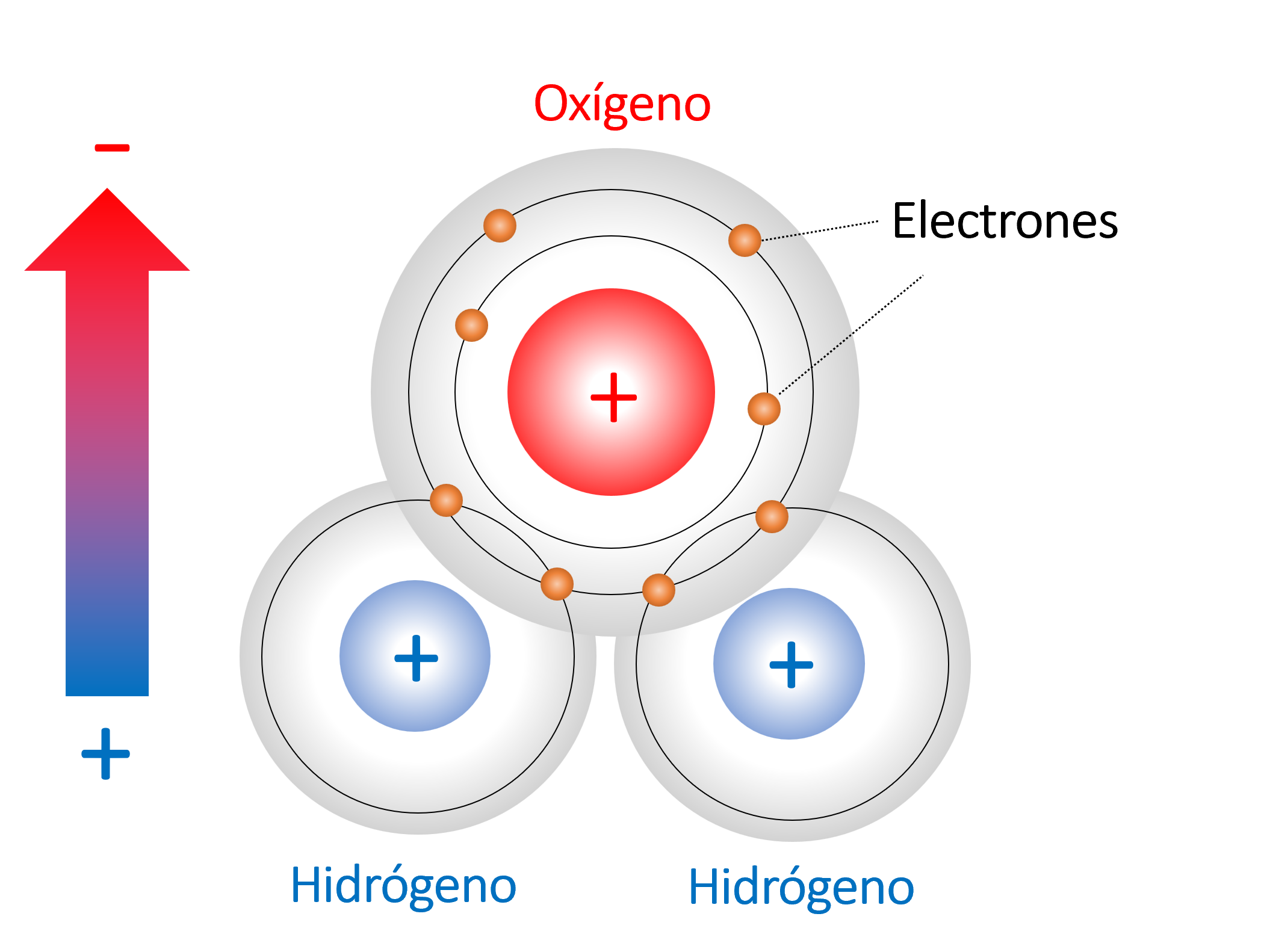
La molécula está polarizada, es decir, posee una carga eléctrica neta positiva en un extremo y negativa en otro.

Esto ocurre debido a que los electrones se mantienen, preferentemente, en la región cercana al núcleo del oxígeno.

El enlance entre el hidrógeno y oxígeno genera una fuerza de atracción, la cual es contrarestada por la repulción entre los núcleos. En forma simplificada, podemos representar este fenómeno mediante un sistema masa-resorte.

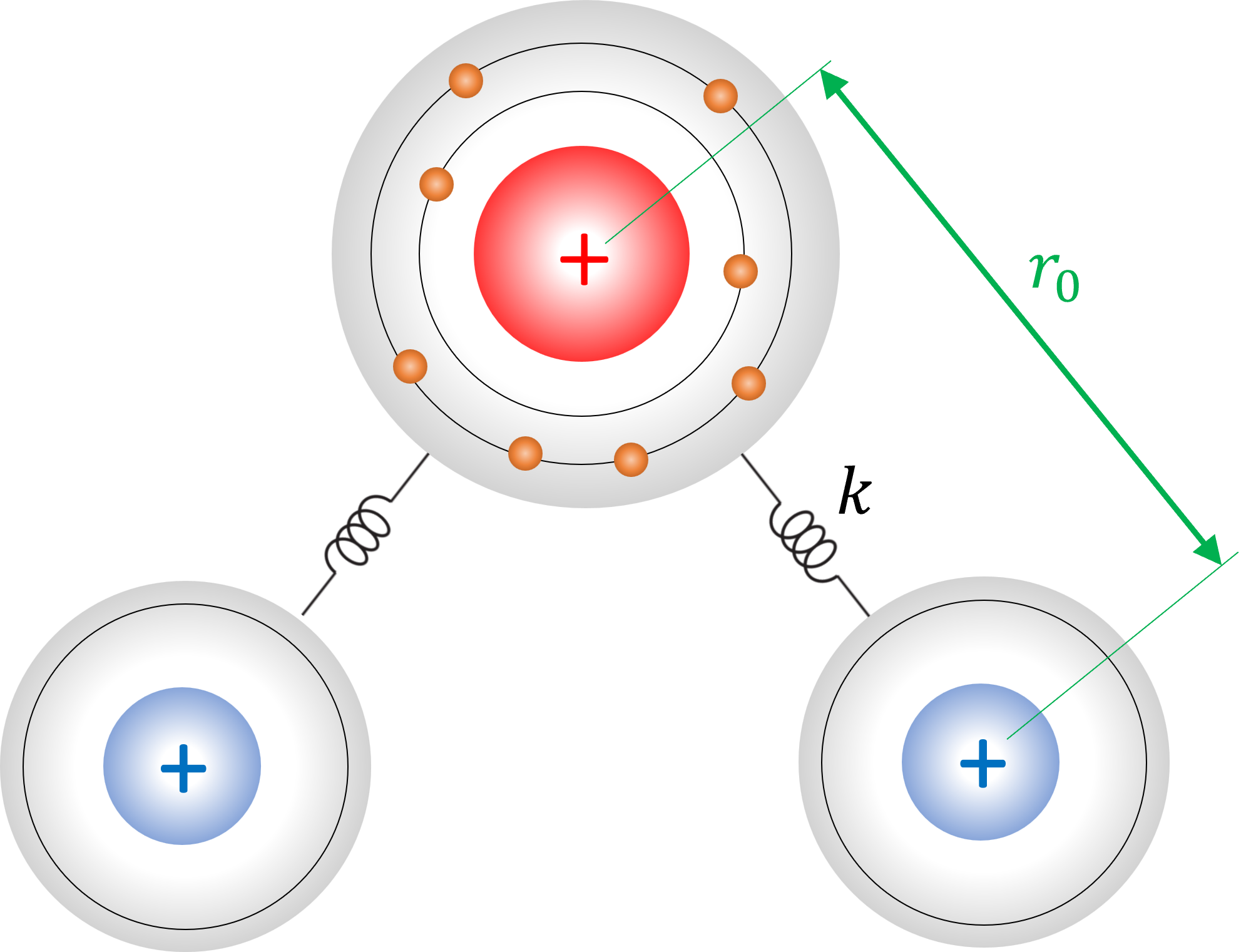
En otras palabras, cada enlace en la molécula de agua representa un oscilador armónico, con una fuerza de restauración:

\[\begin{equation*} F = -k(r - r_0) \end{equation*}\]

donde \(k\) es la constante de rigidez y \(r_0\) es la posición de los núcleos en equilibrio.

3.2.2. Modelo de Lorentz

Simplificando aún más el analisis, consideremos la molécula de agua como un molécula diatómica y analicemos su interacción de una onda electromagnética.

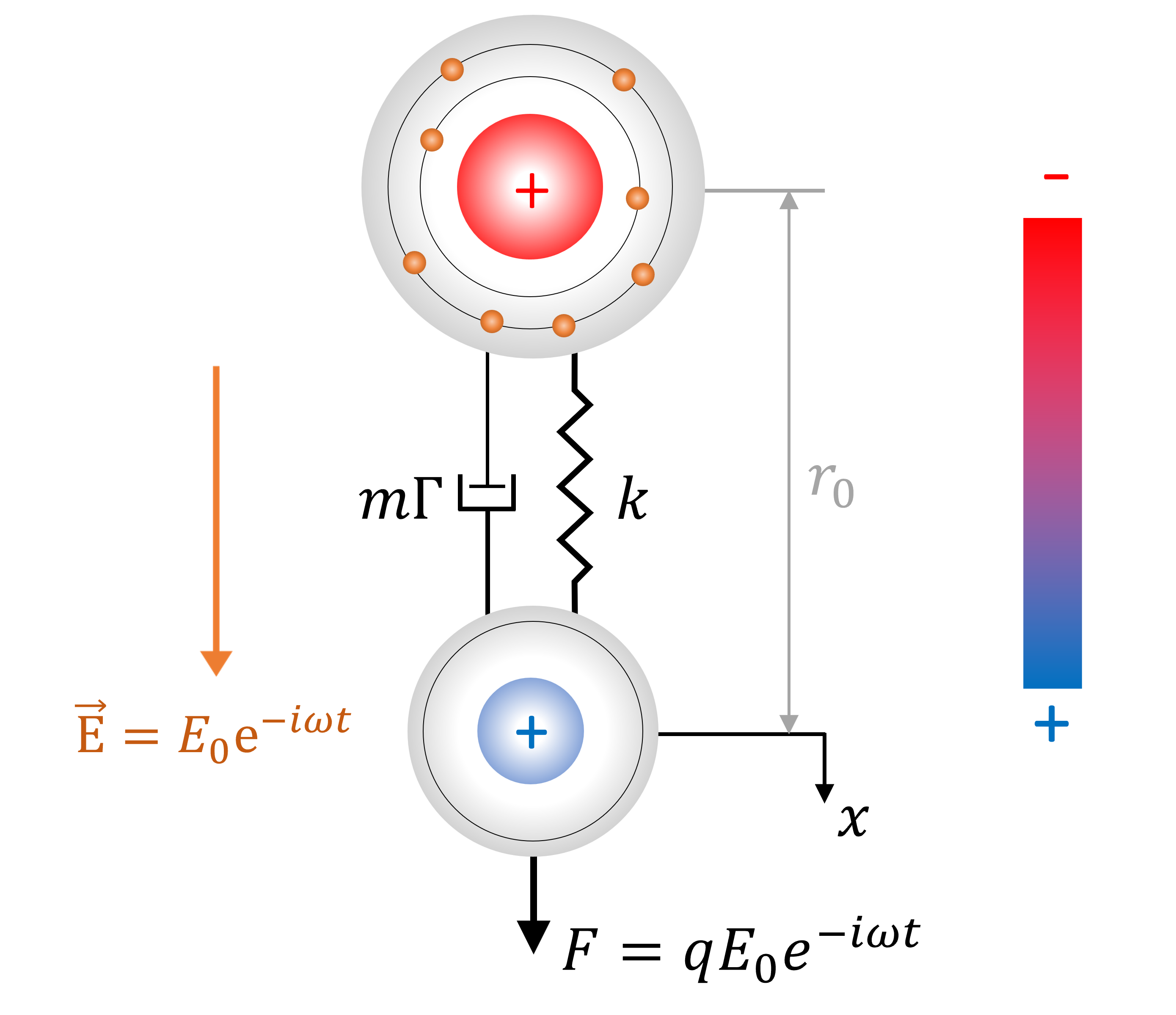
El campo eléctrico de la onda EM (\(E_0e^{-i\omega t}\)), ejerce una fuerza \(F = qE_0e^{-i\omega t}\) sobre cada polo, donde \(q\) es la carga eléctrica del polo positivo (o negativo).

Consideramos, ademas, una fuerza de amortiguación, \(F_{c} = - m\Gamma \dot{x}\), que representa la disipación de energía por la colición entre los electrones y los nucleos, además de otras interacciónes electromagnéticas. La constante \(\Gamma\) es la tasa de decaimiento (se mide en unidades 1/s).

El fenómeno, así, representa un sistema forzado amortiguado

Asumiendo un eje de referencia situado en el polo positivo, la ecuación de movimiento está dada por:

\[\begin{equation*} m\ddot{x} + m\Gamma \dot{x} + k x = qE_0 e^{-i\omega t}, \end{equation*}\]

donde \(m\) es la masa del polo positivo, \(k\) es la constante de rigidez del enlace entre los polos.

La solución estacionaria está dada por la solución particular:

\[\begin{equation*} x_p(t) = \frac{q/mE_0}{\omega_n^2 - \omega^2 - i\Gamma \omega}e^{-i\omega t} \end{equation*}\]

El desplazamiento del polo positivo respecto a su estado en equilibrio induce un momento dipolar, \(\vec{p}\), el cual expresamos a través de la relación:

\[\begin{equation*} \vec{p} = q\vec{x}_p(t) = \frac{q^2/m}{\omega_n^2 - \omega^2 - i\Gamma \omega}E_0e^{-i\omega t}\hat{e}\quad\mathrm{[C\cdot m]} \end{equation*}\]

donde \(\hat{e}\) es la dirección del campo eléctrico

En el caso real, este fenómenos se da en un volumen con millones de moleculas de agua. Considerando que la cantidad de moléculas por unidad de volúmen es \(N_p\), definimos la densidad de polarización, \(\vec{P}\), como el momento dipolar inducido total por unidad de volumen:

\[\begin{equation*} \vec{P} = N_p \vec{p} = \frac{N_pq^2/m}{\omega_n^2 - \omega^2 - i\Gamma \omega}\vec{E}\quad\mathrm{\left[\frac{C\cdot m}{m^3}\right]} \end{equation*}\]

En presencia de un medio polarizado, la ley de Gauss se modifica como: \(\nabla\cdot\left(\varepsilon_0\vec{E} + \vec{P}\right) = 0\).

Representando esta relación en la forma, \(\nabla\cdot\varepsilon_0\varepsilon\vec{E} = \rho\), podemos deducir un modelo para la constante dieléctrica del sistema \(\varepsilon\):

\[\begin{equation*} \varepsilon = 1 +\frac{\omega_p^2}{\omega_n^2 - \omega^2 - i\Gamma \omega}, \end{equation*}\]

con \(\omega_p^2 = \frac{N_pq^2}{\varepsilon_0 m}\)

En el caso del agua, la molecula posee un dipolo eléctrico neto adicional al dipolo inducido. El efecto de la polarización neta se representa, cambiando el primer término por un valor constante \(\varepsilon_\infty\).

El modelo completo se conoce como modelo de Lorentz:

(3.1)\[\begin{equation} \varepsilon = \varepsilon_\infty + \frac{\omega_p^2}{\omega_n^2 - \omega^2 - i\Gamma \omega}\quad\mathrm{Modelo~de~Lorentz}, \end{equation}\]

Usaremos la función lorentz del módulo empylib.nklib para generar el índice de refracción y constante dielectrica a partir del modelo de Lorentz.

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt
import empylib.nklib as nk
import empylib as em

def lorentz_model(epsinf,wn,wp,gamma):
    # espectro 
    lam = np.linspace(1E-3,3,1000)     # convertimos a "micrones"

    # creamos el modelo de lorentz
    N1 = nk.lorentz(epsinf,wp,wn,gamma,lam) # índice de refracción a partir del modelo de Lorentz
    eps1 = N1**2                            # constante dieléctrica

    # formateamos el lienzo para graficar
    fig, ax = plt.subplots(1,2)             # número de ejes en la figura
    fig.set_size_inches(10, 3)              # tamaño de la figura
    plt.rcParams['font.size'] = '10'        # tamaño de fuente

    #ploteamos
    ax[0].plot(lam,eps1.real,'b',label=r"$\varepsilon'$")
    ax[0].plot(lam,eps1.imag,'r',label=r"$\varepsilon''$")
    ax[1].plot(lam,N1.real,'b',label=r"$n$")
    ax[1].plot(lam,N1.imag,'r',label=r"$\kappa$")
    
    # marcar línea de frecuencia natural
    lam_n = em.convert_units(wn,'eV','um')
    ax[0].axvline(x = lam_n, color='k', ls='--', lw='1.0')  
    ax[0].text(lam_n*1.01,-10,'$\omega_n$', fontsize='12', color='k')

    for i in [0,1]:
        ax[i].set_xlabel('Longitud de onda, $\lambda$ ($\mu$m)')
        ax[i].grid()
        ax[i].legend(frameon=False)
        ax[i].set_xlim(0.5,3.0)
    ax[0].set_ylabel(r"Constante dielectrica, $\varepsilon = \varepsilon'+ \varepsilon''$")
    ax[1].set_ylabel(r'Indice de refracción, $N = n + i\kappa$')
    ax[0].set_ylim(-20,30)
    ax[1].set_ylim(0,5)
    plt.show()

Show code cell source Hide code cell source

from ipywidgets import interact

@interact( epsinf=(1,10,0.5), 
           wp=(0.3,1.0,0.1), 
           wn=(0.5,2.0,0.1), 
           gamma=(0.01,0.05,0.005))
def g(epsinf=7,wp=0.8,wn=0.7, gamma=0.04):
    return lorentz_model(epsinf,wn,wp,gamma)

El modelo de Lorentz se utiliza como modelo de ajuste para representar la interacción de la luz con los modos vibratorios en la materia

Por ejemplo, la molécula de agua tiene 3 modos de vibración fundamentales en las longitudes de onda \(\lambda = \) 2.98, 2.93 y 5.91 \(\mu\)m (3351, 3412 y 1691 cm\(^{-1}\))

Ahora, graficamos el índice de refracción del agua medido experimentalmente usando el módulo nklib de la librería empylib.

Show code cell source Hide code cell source

%%capture showplot1
import numpy as np
import matplotlib.pyplot as plt
import empylib.nklib as nk

# Creamos el espectro
lam = np.linspace(0.2,10,1000)                          # espectro de longitudes de onda
N1   = nk.H2O(lam)                                      # índice de refracción
eps1 = N1**2                                            # constante dieléctrica

# Formateamos el lienzo para graficar
fig, ax = plt.subplots(1,2)                             # número de ejes en la figura
fig.set_size_inches(10, 3)                              # tamaño de la figura
plt.rcParams['font.size'] = '12'                        # tamaño de fuente

# Graficamos el resultado
ax[0].plot(lam,eps1.real,'b',label=r"$\varepsilon'$")   # constante dieléctrica (parte real)
ax[0].plot(lam,eps1.imag,'r',label=r"$\varepsilon''$")  # constante dieléctrica (parte imaginaria)
ax[1].plot(lam,N1.real,'b',label=r"$n$")                # índice de refracción (parte real)
ax[1].plot(lam,N1.imag,'r',label=r"$\kappa$")           # índice de refracción (parte imaginaria)

# Marcamos los valores máximos con una línea
for i in [280, 599]:
    ax[0].axvline(x = lam[i], color='k', ls='--', lw='1.0')
    ax[1].axvline(x = lam[i], color='k', ls='--', lw='1.0')
    ax[0].text(lam[i]*1.02,eps1[i].imag,r'%.3f $\mu$m'% lam[i], fontsize='10')

for i in [0,1]:
    ax[i].set_xlabel('Longitud de onda, $\lambda$ ($\mu$m)')
    ax[i].grid()
    ax[i].set_xlim(0.2,10)
    ax[i].legend(frameon=False)
ax[0].set_ylabel(r"Constante dielectrica, $\varepsilon = \varepsilon'+ \varepsilon''$")
ax[1].set_ylabel(r'Indice de refracción, $N = n + i\kappa$')
plt.show()

Show code cell source Hide code cell source

showplot1()

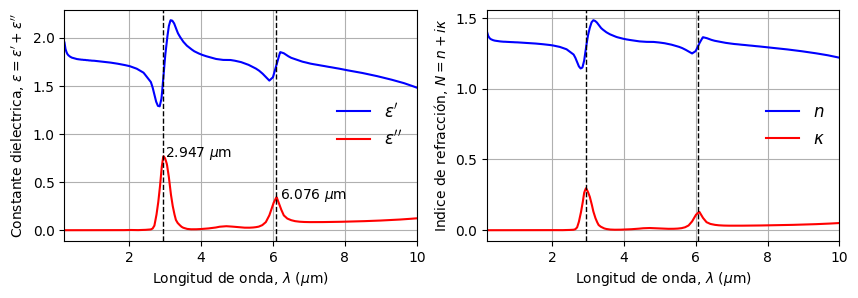
De la figura notamos dos oscilaciones de Lorentz. El modo de resonancia en \(\lambda =\) 2.98 \(\mu\)m (3351 cm\(^{-1}\)) no está presente en el espectro.

Este modo no es compatible con la oscilación de una onda electromagnética plana. Así la luz no interactúa con esta vibración y, por lo tanto, no se ve representada en el espectro del índice de refracción.

En síntesis, la forma del índice de refracción de cada material es el resultado de la interacción de las ondas electromagnéticas con los modos vibratórios de las moléculas. Cada peak en la curva de \(\kappa\) indica que la luz ha activado un modo de resonancia de la molécula. En estos puntos, la amplitud de la luz decae, lo que significa que la energía de la luz es transferida a la molécula.

3.3. Interacción de la luz con sólidos

El análisis anterior se aplica a gases, donde la interacción entre moléculas es débil. En el caso de materiales sólidos, la interacción entre moléculas es fuerte y se comporta como un sistema con múltiples grados de libertad. Los electrones, que también forman parte de ese sistema, ven modificados sus estados de energía (o modos de vibración). Cada orbital (que representa un estado de energía), se convierte en una banda que será ocupada por los electrones disponibles.

Llamamos nivel de Fermi, a la máxima energía ocupada por los electrones. En base a este límite, destacamos tres bandas de energía:

• Banda de valencia: corresponde a la banda ocupada por electrones con el mayor nivel de energía. En esta banda los electrones permanecen en un estado “ligado” al núcleo.

• Banda de conducción: corresponde a la banda no ocupada por electrones con el menor nivel de energía. En esta banda los electrones se mueven líbremente por el material

• Banda prohibida (band-gap): Es la diferencia entre la banda de conducción y la banda de valencia

La separación entre la banda de conducción y la banda de valencia es fundamental en el comportamiento electrónico del material.

Podemos clasificar tres tipos:

• Conductor, donde las bandas de conducción y valencia están traslapadas (\(E_\mathrm{g} = 0\)). En estos materiales, parte de los electrones están alojados en la banda de conducción y, por lo tanto, son capaces de conducir corriente eléctrica en presencia de un campo eléctrico.

• Semiconductor, donde las bandas de conducción y valencia están separadas. La energía del bandgap es relativamente pequeña, de manera que un electrón puede ser llevado a la banda de conducción mediante un potencial eléctrico razonable, o mediante un fotón con energía \(h\nu > E_\mathrm{g}\) (comúnmente del espectro uv o visible).

• Aislante, donde las bandas de conducción y valencia están muy separadas. El umbral para excitar un electrón a la banda de conducción es demaciado grande y, por lo tanto, el material no es capaz de conducir corriente. Así mismo, el material no es capaz de absorber fotones en el uv o visible.

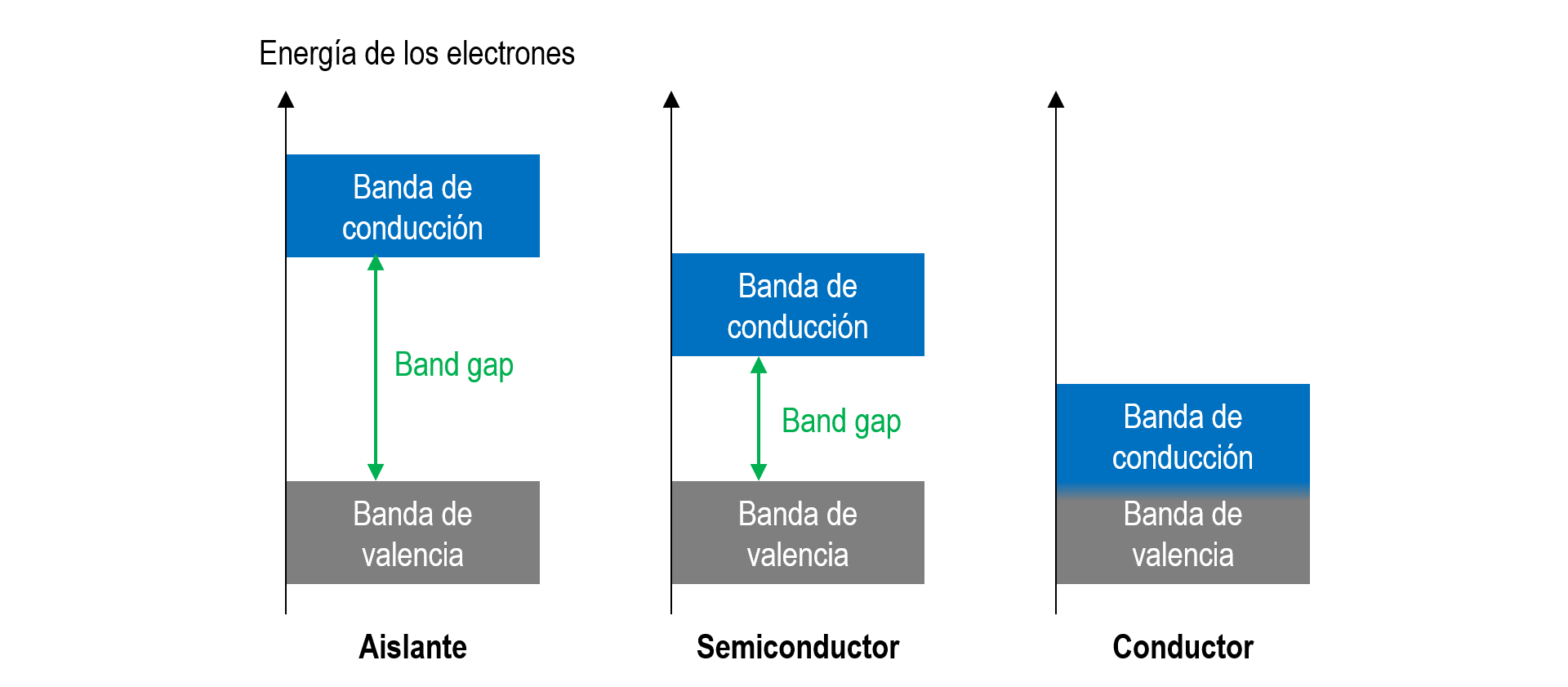
La respuesta óptica de cada tipo de material está condicionada por sus propiedades electrónicas.

3.3.1. Aislantes (modelo de Lorentz)

En este caso, \(E_\mathrm{g}\) es muy alto y el material no presenta absorción a radiación uv o visible. La respuesta óptica está condicionada, únicamente, por la interacción con los modos de vibración de la red de moléculas. El modelo de Lorentz, así, representa una buena aproximación para representar \(\varepsilon\) o \(N\).

Un buen ejemplo es el sílice (SiO\(_2\)), cuya estructura puede ser de tipo cristalina o amorfa.

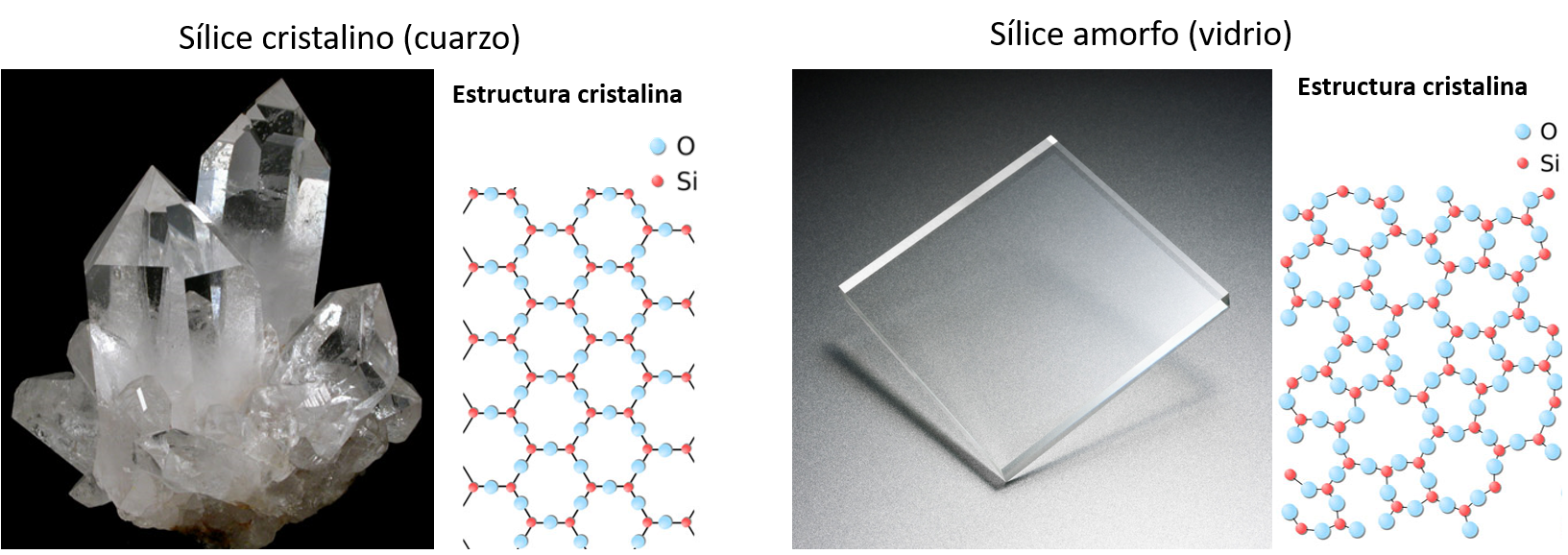
A continuación, usaremos la librería empylib para graficar el índice de refracción y constante dieléctrica del sílice obtenidos de forma experimental. Notar los peaks caracteristicos del modelo de Lorentz que representan la excitación de los modos de vibración de la red molecular.

Show code cell source Hide code cell source

%%capture showplot1
import numpy as np
import matplotlib.pyplot as plt
import empylib.nklib as nk

lam = np.linspace(0.2,30,1000)                          # espectro de longitudes de onda
N1   = nk.SiO2(lam)                                     # índice de refracción
eps1 = N1**2                                            # constante dieléctrica

# formateamos el lienzo para graficar
fig, ax = plt.subplots(1,2)                             # número de ejes en la figura
fig.set_size_inches(10, 3)                              # tamaño de la figura
plt.rcParams['font.size'] = '10'                        # tamaño de fuente

# Graficamos el resultado
ax[0].plot(lam,eps1.real,'b',label=r"$\varepsilon'$")   # constante dieléctrica (parte real)
ax[0].plot(lam,eps1.imag,'r',label=r"$\varepsilon''$")  # constante dieléctrica (parte imaginaria)
ax[1].plot(lam,N1.real,'b',label=r"$n$")                # índice de refracción (parte real)
ax[1].plot(lam,N1.imag,'r',label=r"$\kappa$")           # índice de refracción (parte imaginaria)

for i in [0,1]:
    ax[i].set_xlabel('Longitud de onda, $\lambda$ ($\mu$m)')
    ax[i].grid()
    ax[i].legend(frameon=False)
ax[0].set_ylabel(r"Constante dielectrica, $\varepsilon = \varepsilon'+ \varepsilon''$")
ax[1].set_ylabel(r'Indice de refracción, $N = n + i\kappa$')
plt.show()

showplot1()

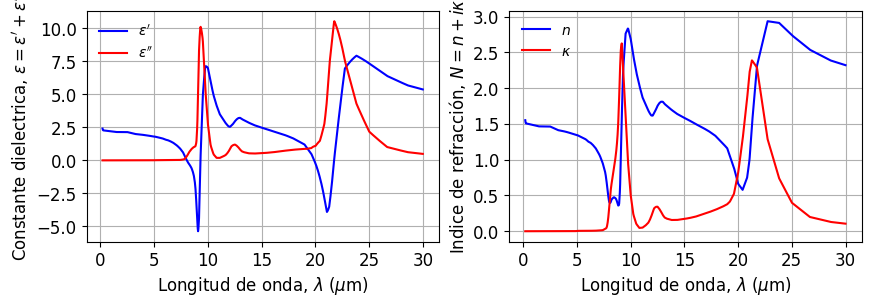
3.3.2. Conductores (modelo de Drude)

En este caso los electrones se mueven libremente por la red atómica.

La interacción entre estos electrones y una onda electromagnética puede ser modelada como un movimiento forzado sin fuerza de restauración (\(kx = 0\)):

\[\begin{equation*} m_e\ddot{x} + m_e\Gamma_e \dot{x} = eE_0 e^{-i\omega t}, \end{equation*}\]

donde \(m_e\), \(e\) y \(\Gamma_e\) son, respectivamente, la masa, la carga elemental y la taza de decaimiento del electrón.

Mediante un procedimiento similar al utilzado para el modelo de Lorentz podemos derivar el modelo de Drude para conductores:

(3.2)\[\begin{equation} \varepsilon = \varepsilon_\infty - \frac{\omega_p^2}{\omega^2 + i\Gamma_e \omega},\quad\mathrm{Modelo~de~Drude}, \end{equation}\]

donde \(\omega_p^2 = \frac{N_ee^2}{\varepsilon_0 m}\) se conoce como frecuencia de plasma, y \(N_e\) es la densidad de número de electrones. Similar al modelo de Lorentz, \(\varepsilon_\infty\) representa la polarización neta del material.

Usaremos la función drude del módulo empylib.nklib para generar el índice de refracción y constante dielectrica a partir del modelo de Drude. En el gráfico marcamos el equivalente a \(\omega_p\) en longitud de onda \(\lambda_p = 2\pi c_0/\omega_p\).

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt
import empylib.nklib as nk
import empylib as em

def drude_model(epsinf,wp,gamma):
    lam = np.linspace(1E-3,5,1000)    # longitudes de onda

    # contruimos el modelo de Drude
    N1 = nk.drude(epsinf,wp,gamma,lam)     # índice de refra]cción
    eps1 = N1**2                           # constante dieléctrica

    # formateamos el lienzo para graficar
    fig, ax = plt.subplots(1,2)             # número de ejes en la figura
    fig.set_size_inches(10, 3)              # tamaño de la figura
    plt.rcParams['font.size'] = '10'        # tamaño de fuente

    # graficamos constante dielectrica e índice de refracción
    ax[0].plot(lam,eps1.real,'b',label=r"$\varepsilon'$")
    ax[0].plot(lam,eps1.imag,'r',label=r"$\varepsilon''$")
    ax[1].plot(lam,N1.real,'b',label=r"$n$")
    ax[1].plot(lam,N1.imag,'r',label=r"$\kappa$")
    
    # marcar línea de frecuencia natural
    lam_p = em.convert_units(wp,'eV','um')
    ax[0].axvline(x = lam_p, color='k', ls='--', lw='1.0')  
    ax[0].text(lam_p*1.1,-9,r'$\lambda_p =%.3f$ $\mu$m' % lam_p, fontsize='10', color='k')

    for i in [0,1]:
        ax[i].set_xlabel('Longitud de onda, $\lambda$ ($\mu$m)')
        ax[i].grid()
        ax[i].legend(frameon=False)
        ax[i].set_xlim(0,5.0)
    ax[0].set_ylabel(r"Constante dielectrica, $\varepsilon = \varepsilon'+ \varepsilon''$")
    ax[1].set_ylabel(r'Indice de refracción, $N = n + i\kappa$')
    ax[0].set_ylim(-10,10)
    ax[1].set_ylim(0,5)
    plt.show()

Show code cell source Hide code cell source

from ipywidgets import interact

@interact( epsinf=(1,5,0.1), 
           wp=(0.4,2.0,0.05), 
           gamma=(0.01,0.2,0.01))
def g(epsinf=1,wp=1.0, gamma=0.1):
    return drude_model(epsinf,wp,gamma)

Notar que la condición \(\varepsilon' < 0\) se manifiesta en el índice de refracción como \(\kappa > n\) y ocurre cuando \(\lambda_p \lesssim \lambda\)

En la región \(\kappa > n\), la reflectividad aumenta significativamente. Esto explica la alta reflectividad en los conductores eléctricos

Show code cell source Hide code cell source

%%capture showplot3

import numpy as np
import matplotlib.pyplot as plt
from empylib.waveoptics import interface
import empylib as em
import empylib.nklib as nk

def drude_reflection(epsinf,wp,gamma):
    lam = np.linspace(1E-3,5,1000)    # longitudes de onda

    # contruimos el modelo de Drude
    n2 = nk.drude(epsinf,wp,gamma,lam)     # índice de refracción
    
    # índice de refracción aire
    n1 = np.ones(n2.shape)                    

    # Reflectividad en una interface entre un material de Drude y aire
    Rp = interface(0,n1,n2, pol='TM')[0] # TM
    Rs = interface(0,n1,n2, pol='TE')[0] # TE

    # formateamos el lienzo para graficar
    fig, ax = plt.subplots(1,2)             # número de ejes en la figura
    fig.set_size_inches(10, 3)              # tamaño de la figura
    plt.rcParams['font.size'] = '10'        # tamaño de fuente

    # graficamos constante dielectrica e índice de refracción
    ax[0].plot(lam,n2.real,'b',label=r"$n$")
    ax[0].plot(lam,n2.imag,'r',label=r"$\kappa$")
    ax[1].plot(lam,Rp, label='$R_\mathrm{TM}$', color='red', lw=3.0)
    ax[1].plot(lam,Rs, label='$R_\mathrm{TE}$', color='blue', lw=2.0, ls='--')
    
    
    # marcar línea de frecuencia natural
    lam_p = em.convert_units(wp,'eV','um')
    ax[0].axvline(x = lam_p, color='k', ls='--', lw='1.0')  
    ax[0].text(lam_p*1.1,4,r'$\lambda_p =%.3f$ $\mu$m' % lam_p, fontsize='10', color='k')
    
    ax[1].axvline(x = lam_p, color='k', ls='--', lw='1.0')  
    ax[1].text(lam_p*1.1,0.2,r'$\lambda_p =%.3f$ $\mu$m' % lam_p, fontsize='10', color='k')

    for i in [0,1]:
        ax[i].set_xlabel('Longitud de onda, $\lambda$ ($\mu$m)')
        ax[i].grid()
        ax[i].legend(frameon=False)
        ax[i].set_xlim(0,5.0)
    ax[0].set_ylabel(r'Indice de refracción, $N = n + i\kappa$')
    ax[1].set_ylabel('Reflectividad')
    ax[0].set_ylim(0,5)
    ax[1].set_ylim(0,1.0)
    plt.show()

Show code cell source Hide code cell source

from ipywidgets import interact

@interact( epsinf=(1,5,0.1), 
           wp=(0.4,2.0,0.05), 
           gamma=(0.01,0.2,0.01))
def g(epsinf=1,wp=1.0, gamma=0.1):
    return drude_reflection(epsinf,wp,gamma)

Los metales pueden ser bien representados por el modelo de Drude. En general, \(\omega_p\) se ubica en el espectro UV, lo que significa que el metal reflejará la luz visible (efecto espejo)

Por ejemplo, en el caso de aluminio \(\omega_p = 15~\mathrm{eV}\approx 90~\mathrm{nm}\)

Show code cell source Hide code cell source

%%capture showplot4
import numpy as np
import matplotlib.pyplot as plt
import empylib.nklib as nk

# índice de refracción y constante dielectrica aluminio
lam = np.linspace(0.01,1.0,1000)        # espectro de longitudes de onda (um)
N1 = nk.Al(lam)                         # índice de refracción
eps1 = N1**2                            # constante dieléctrica

# formateamos el lienzo para graficar
fig, ax = plt.subplots(1,2)             # número de ejes en la figura
fig.set_size_inches(10, 3)              # tamaño de la figura
plt.rcParams['font.size'] = '10'        # tamaño de fuente

# graficamos
ax[0].plot(lam,eps1.real,'b',label=r"$\varepsilon'$")
ax[0].plot(lam,eps1.imag,'r',label=r"$\varepsilon''$")
ax[1].plot(lam,N1.real,'b',label=r"$n$")
ax[1].plot(lam,N1.imag,'r',label=r"$\kappa$")

# formateamos los ejes
for i in [0,1]:
    ax[i].set_xlabel('Longitud de onda, $\lambda$ ($\mu$m)')
    ax[i].grid()
    ax[i].set_xlim(0.01,1.0)
    ax[i].legend(frameon=False)
ax[0].set_ylabel(r"Constante dielectrica, $\varepsilon = \varepsilon'+ \varepsilon''$")
ax[1].set_ylabel(r'Indice de refracción, $N = n + i\kappa$')
plt.show()

Show code cell source Hide code cell source

showplot4()

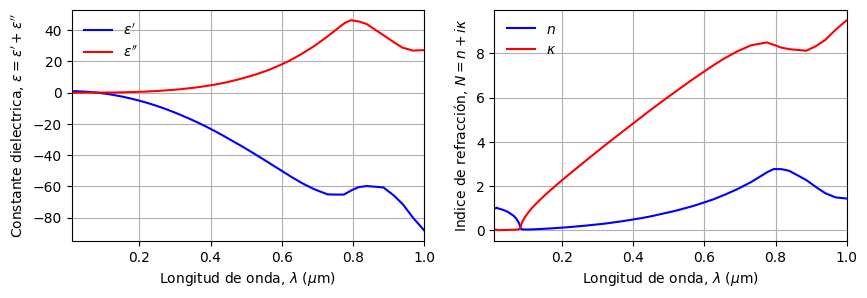
Notemos como para \(\lambda \approx 0.8\) \(\mu\)m, la respuesta del material se desvía del modelo de Drude. Esta respuesta esta asociada a un modo de vibración (modelo de Lorentz).

3.3.3. Semiconductores (absorción interbanda)

En este caso, el material presentará absorción de fotones debido a la excitación de electrones de la banda de valencia a la banda de conducción.

Este fenómeno se conoce como absorpción interbanda.

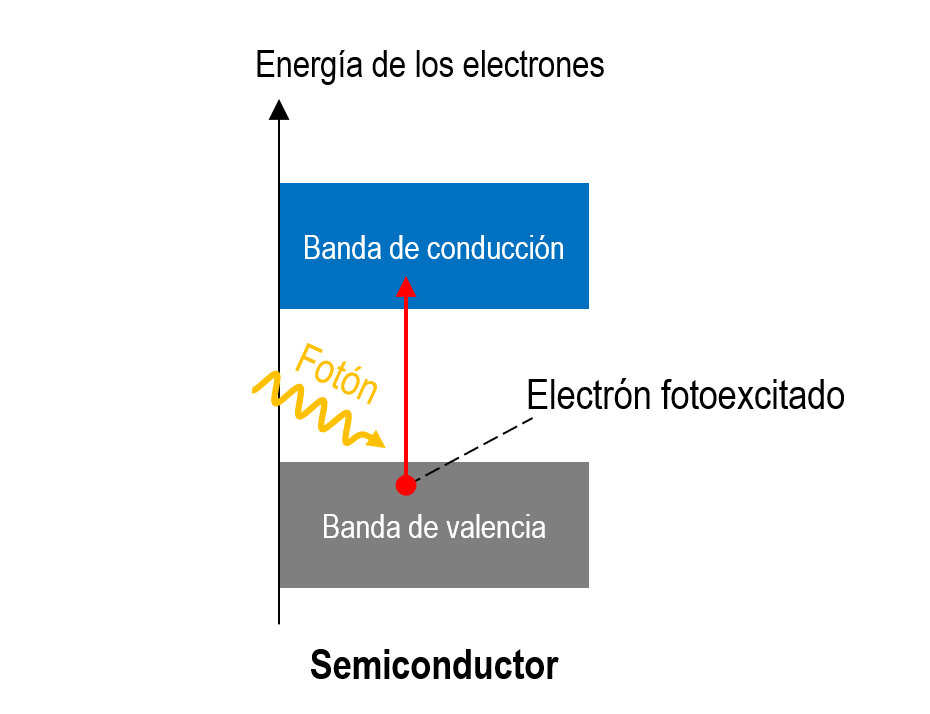
Los semiconductores son los materiales fundamentales en transistores, LED y celdas fotovoltaicas. El más conocido es el silicio (Si).

Al graficar el índice de refracción del silicio, notamos que la extinsión \(\kappa\) aumenta significativamente para \(\lambda < 0.4 \mu\mathrm{m}\). Este límite corresponde al bandgap del material.

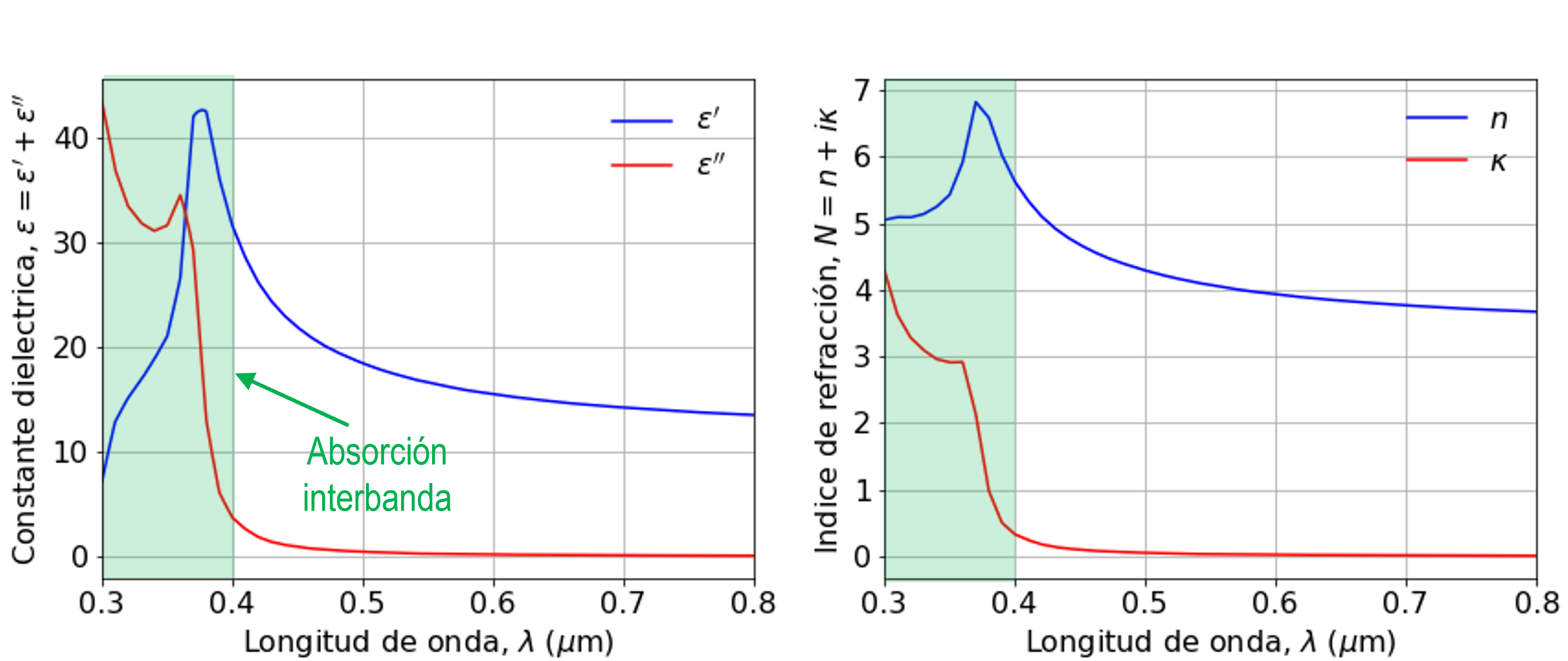
En general, los materiales pueden presentar más de un tipo de respuesta. Por ejemplo, el oro tiene absorción interbanda en longitudes de onda \(\lambda < 0.5\) \(\mu\)m, combinado con el modelo de Drude.

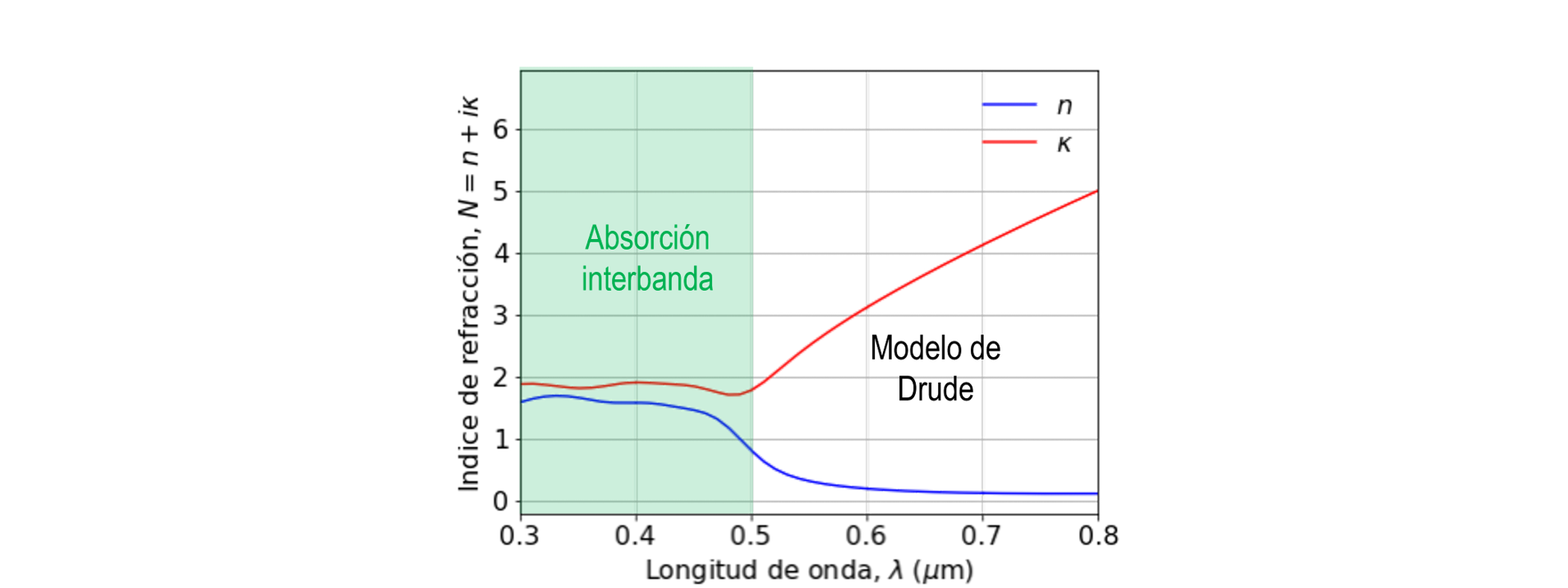
Debido a esta respuesta, el oro absorbe las longitudes de onda correspondientes al azul y violeta, y refleja el resto de los colores.

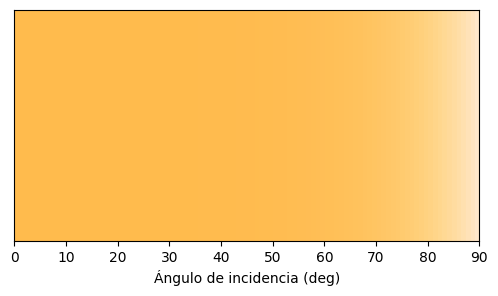
La siguiente figura muestra el color del oro según el ángulo de incidencia en base al espectro de reflexión de una interface aire/oro.

Show code cell source Hide code cell source

%%capture showplot5
import numpy as np
import matplotlib.pyplot as plt
from empylib.waveoptics import interface
from empylib.ref_spectra import AM15
import empylib.color_system as cs
cs = cs.hdtv

# creamos índices de refracción
lam = np.linspace(0.3,0.8,81)   # espectro de longitudes de onda (en um)
n2 = nk.gold(lam)               # índice de refracción oro
n1 = np.ones(n2.shape)          # índice de refracción aire

# Reflectividad en interface función del ángulo "tt"
Rp = lambda tt : interface(tt, n1,n2, pol='TM')[0]
Rs = lambda tt : interface(tt, n1,n2, pol='TE')[0]

# formateamos la figura
fig, ax = plt.subplots()                # número de ejes en la figura
fig.set_size_inches(6, 3)               # tamaño de la figura
plt.rcParams['font.size'] = '12'        # tamaño de fuente        

# graficamos el color reflejado según el ángulo de incidencia
theta = np.linspace(0,90,100)           # angulo de incidencia
for i in range(len(theta)): 
    R = 0.5*Rp(np.radians(theta[i])) + 0.5*Rs(np.radians(theta[i]))
    Irad = R*AM15(lam)
    html_rgb = cs.spec_to_rgb(Irad, lam, out_fmt='html')
    ax.axvline(theta[i], color=html_rgb, linewidth=6) 
ax.set_xlim([min(theta),max(theta)])
ax.set_ylim([0,1.0])
ax.axes.yaxis.set_visible(False)
ax.set_xlabel('Ángulo de incidencia (deg)')
plt.show()

Show code cell source Hide code cell source

showplot5()

Otro ejemplo es el dioxido de titanio (TiO\(_2\)), el cual presenta absorción interbanda en el espectro ultravioleta, y oscilaciones de Lorentz en el infrarojo.

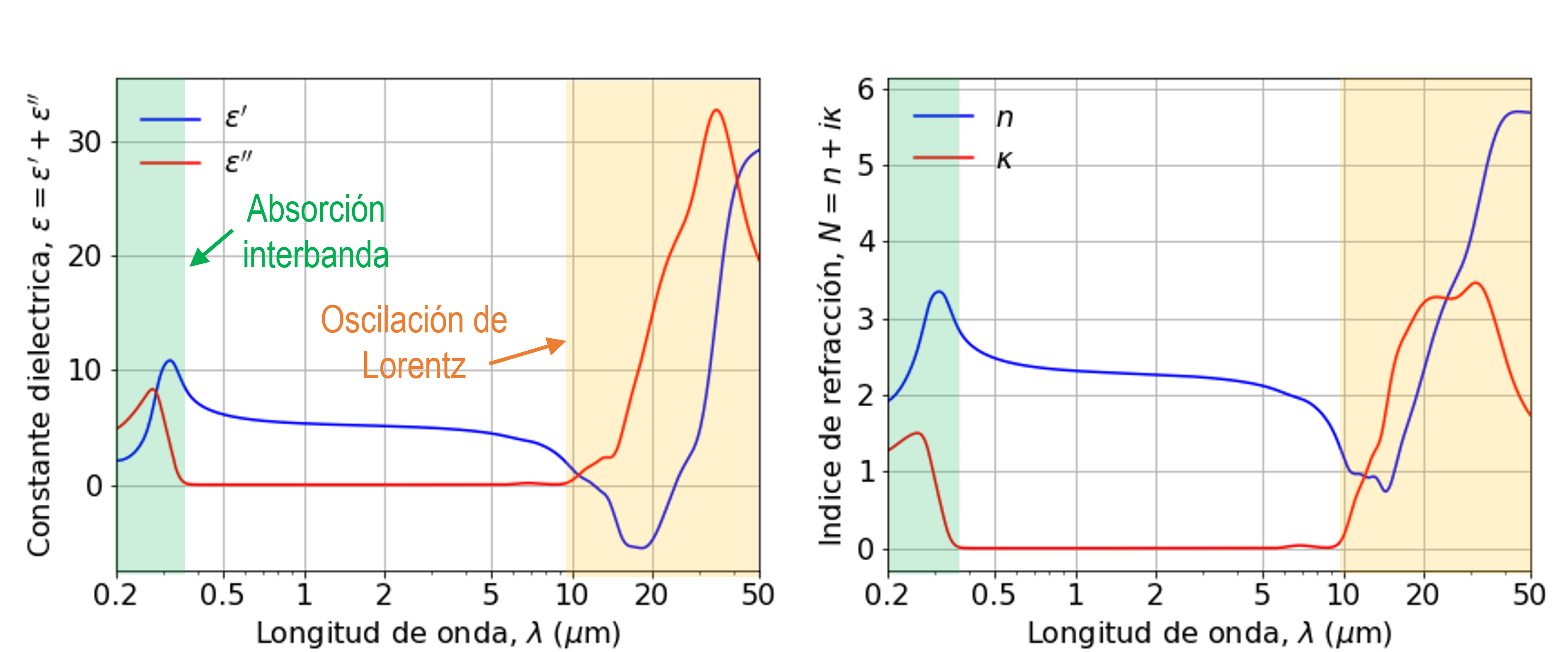
Debido a la absorcion UV, TiO\(_2\) es muy utilizado en cremas para protección solar.

También es utilizado como catalizador de hidrógeno mediante la fotoreducción de agua

3.4. Referencias

• Rao S. S. Chapter 4 - Vibration Under General Forcing Conditions in Mechanical Vibrations, 6th Ed, Pearson, 2018

• Griffths D., Chapter 4.1 - Polarization in Introduction to Electrodynamics, 4th Ed, Pearson, 2013

• Simmons J. and Potter K., Chapter 2 and 3 in Optical Materials, 1st Ed, Academic Press, 2000