Radiación Solar

7. Radiación Solar#

7.1. Ángulos solares#

7.1.1. Características de la órbita de la tierra#

  • La órbita de la tierra aproximadamente circular, con una pequeña excentricidad (\(e = 1.673\)%).

  • La distancia entre el sol y la tierra está dada por: \(d_\mathrm{e-s} = 1.495\times 10^{11}~\mathrm{m}\pm 1.7\)%.

  • El eje de la tierra está inclinado 23.45° del plano ecliptico (plano de la órbida de la tiera)

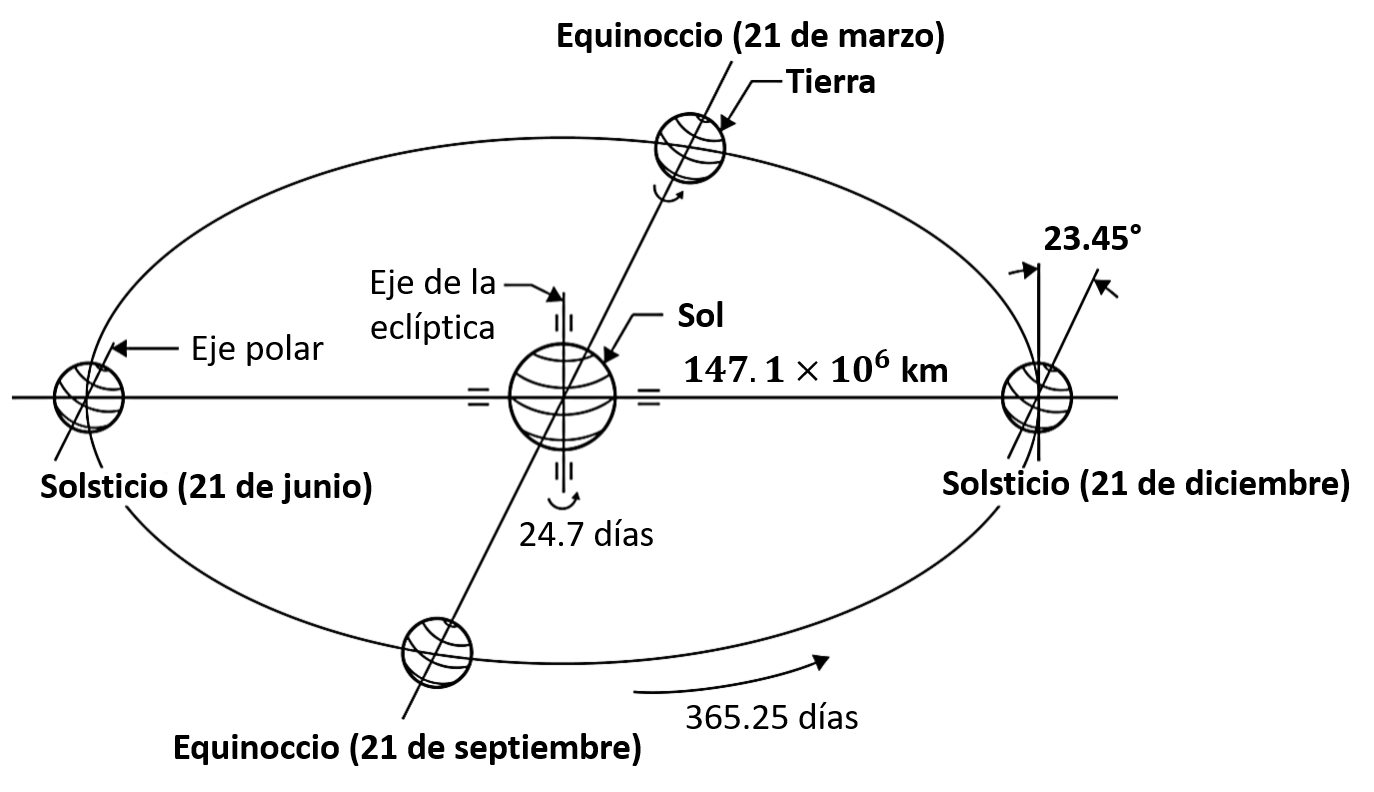
../_images/earth_orbit.png

7.1.2. Trayectoria del sol#

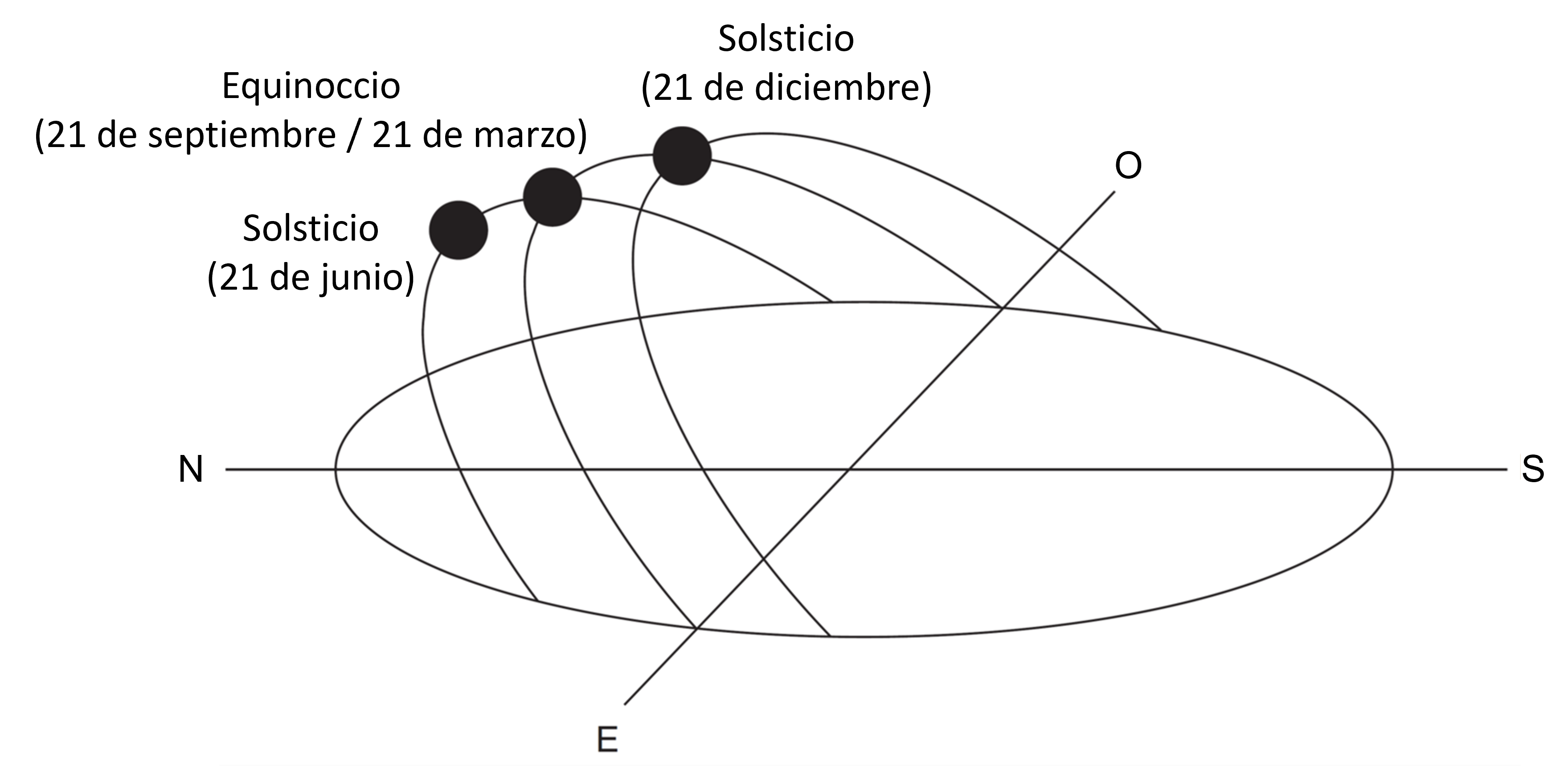
A raíz de estas caracteristicas, la trayectoria del sol vista desde la tierra forma un arco. En el hemisferio sur de la tierra, este arco aparece desplazado hacia el norte(sur) del eje Este-Oeste en el solsticio del 21 de junio (21 de diciembre). En el hemisferio norte ocurre lo opuesto. Durante los equinoccios el arco está centrado en el eje Este-Oeste independiente del lado del hemisferio.

../_images/sun_trayectory.png

7.1.3. Posición del sol en coordenadas ecuatoriales#

Utilizando el plano ecuatorial como referencia, podemos definir la posición del sol respecto a dos ángulos, declinación solar y ascención recta

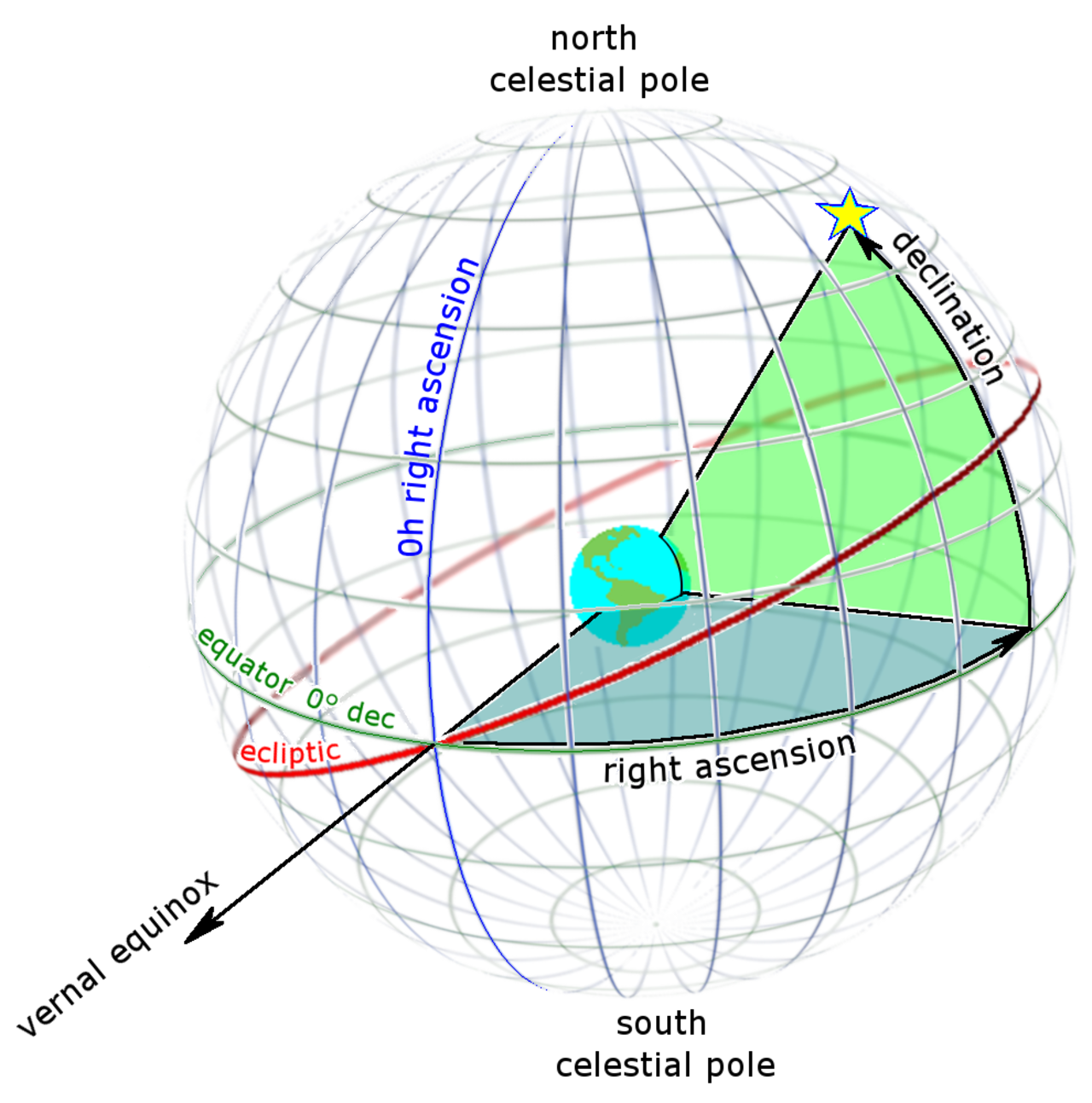
../_images/solar_position_ecuator.png

  • La declinación solar, \(\delta\) corresponde al ángulo vertical medido desde el plano ecuatorial.

  • La ascención recta, \(\mathrm{AR}\) se define como el ángulo horizontal en referencia al eje del equinoccio vernal (21 de marzo), también conocido como punto de aries. Se mide en horas, con 1 hora equivalente a 15°.

En el equinoxio del 21 de marzo, \(\delta \approx 0°\) y \(\mathrm{AR}\approx 0\) h

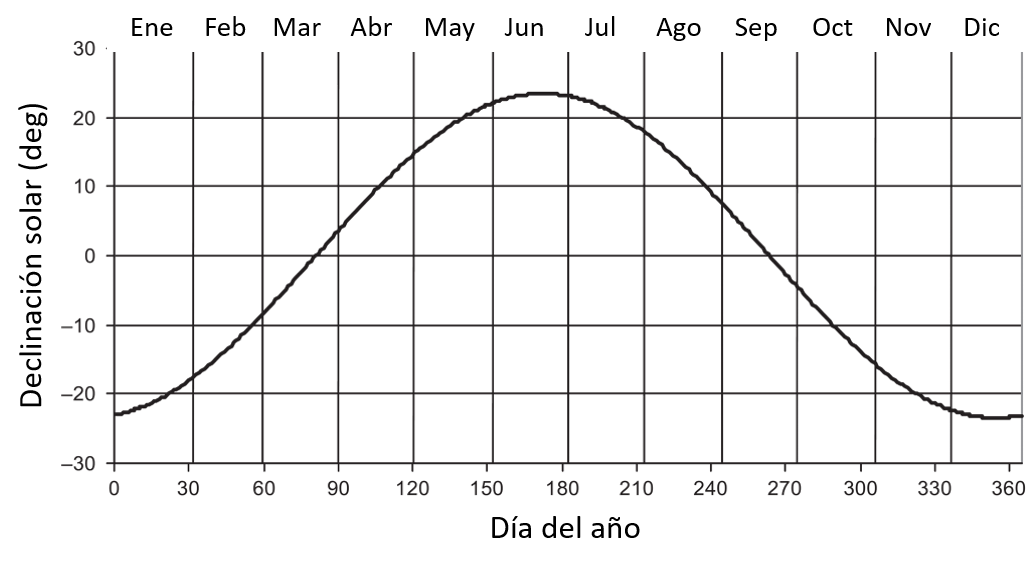
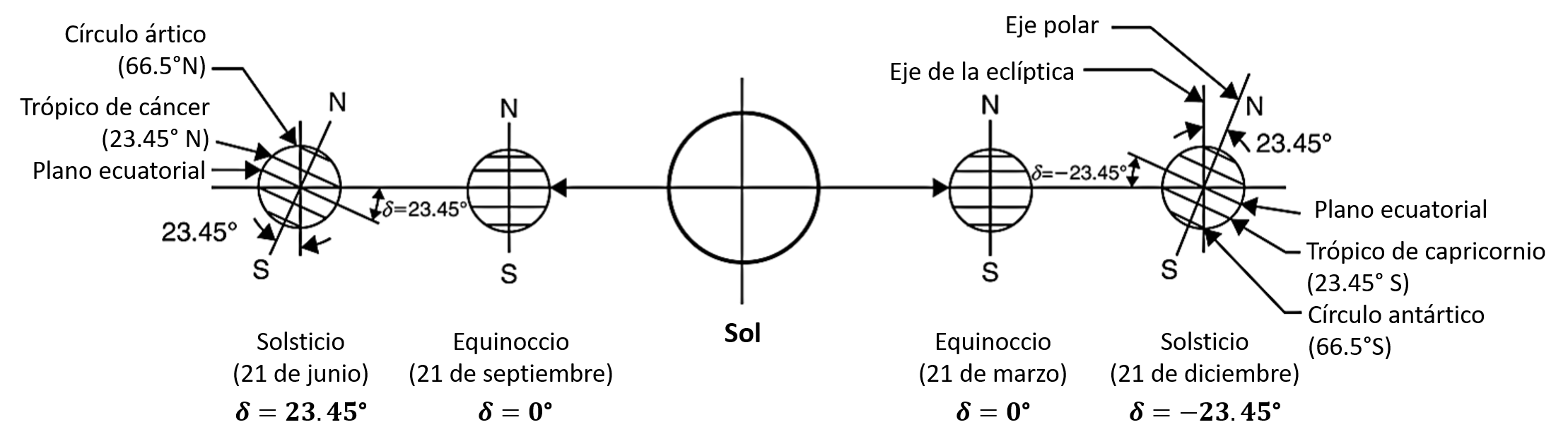
La declinación solar esta asociada con la inclinación del eje polar respecto al plano eclíptico. ../_images/schematic_declination.png

../_images/declination_year.png

7.1.4. Posición del sol respecto al plano horizontal local#

Una forma más intuitiva de definir la posición del sol, es utilizando el plano horizontal local. En este caso, caracterizamos la posición del sol respecto a los ángulos, elevación solar (\(\alpha_\mathrm{s}\)) y acimut solar (\(\phi_\mathrm{s}\)).

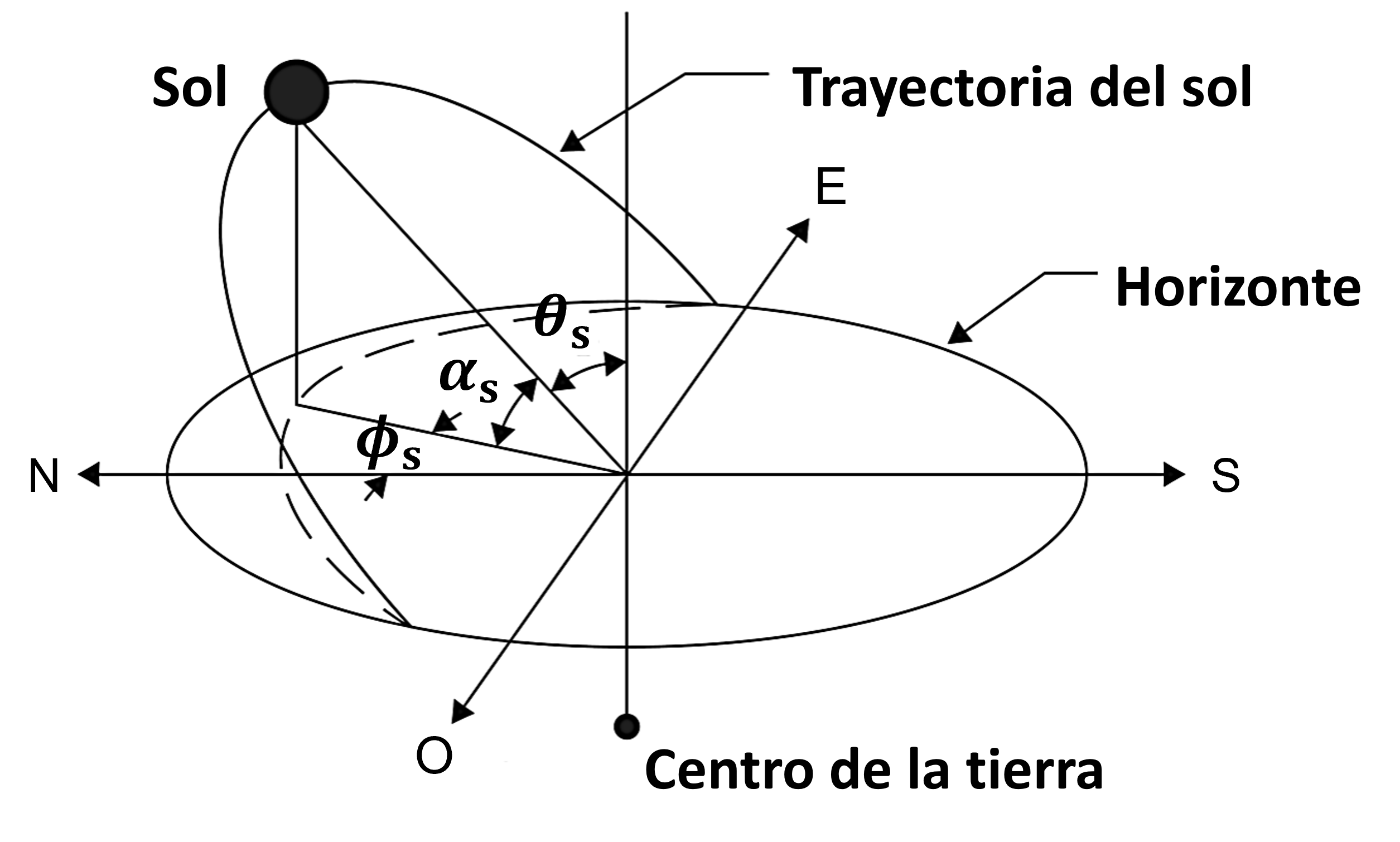
../_images/solar_position_horizon.png

  • El ángulo de elevación solar, \(\alpha_\mathrm{s}\), corresponde a la posición del sol respecto al plano perpendicular al horizonte local. Su valor es complementario al ángulo cenital solar \(\theta_\mathrm{s} = \pi/2 - \alpha_\mathrm{s}\).

  • El ángulo acimut solar \(\phi_\mathrm{s}\) mide la proyección de la posición del sol en el plano horizontal local. El valor \(\phi_\mathrm{s} = 0\)°, corresponde al eje norte creciendo en dirección este.

El valor de \(\alpha_\mathrm{s}\) y \(\phi_\mathrm{s}\), es función de \(\delta\), \(\mathrm{AR}\), la longitud, latitud y la hora local.

En este curso utilizaremos \(\alpha_\mathrm{s}\) y \(\phi_\mathrm{s}\) directamente utilizando fuentes disponibles en línea.

7.1.5. Ángulo de incidencia#

El ángulo de incidencia del sol, \(\theta_\mathrm{i}\), corresponde al ángulo cenital relativo a la normal de una superficie. En la siguiente figura se muestra una superficie inclinada con ángulo cenital \(\beta\) y ángulo acimutal \(\Phi\) respecto a la dirección normal al plano horizontal

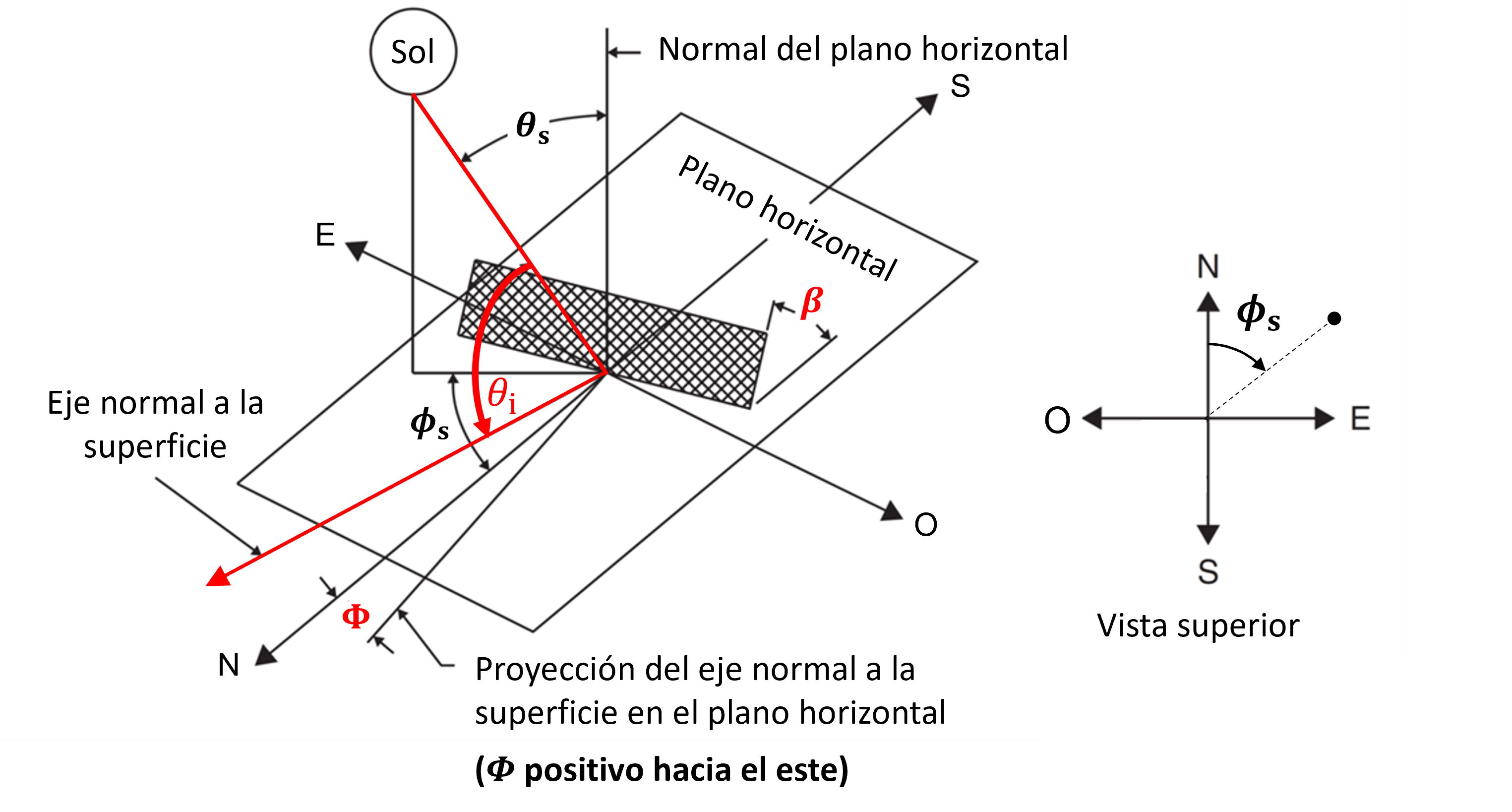
../_images/incidence_angle.png

Considerando la posición del sol relativa al plano horizontal, el ángulo de incidencia es:

(7.1)#\[\begin{equation} \cos\theta_i = \cos\theta_\mathrm{s}\cos\beta+\sin\theta_\mathrm{s}\sin\beta\cos(\phi_\mathrm{s} - \Phi) \end{equation}\]

Para una superficie en posición horizontal, \(\theta_\mathrm{i} = \theta_\mathrm{s}\)

7.2. Radiación solar disponible#

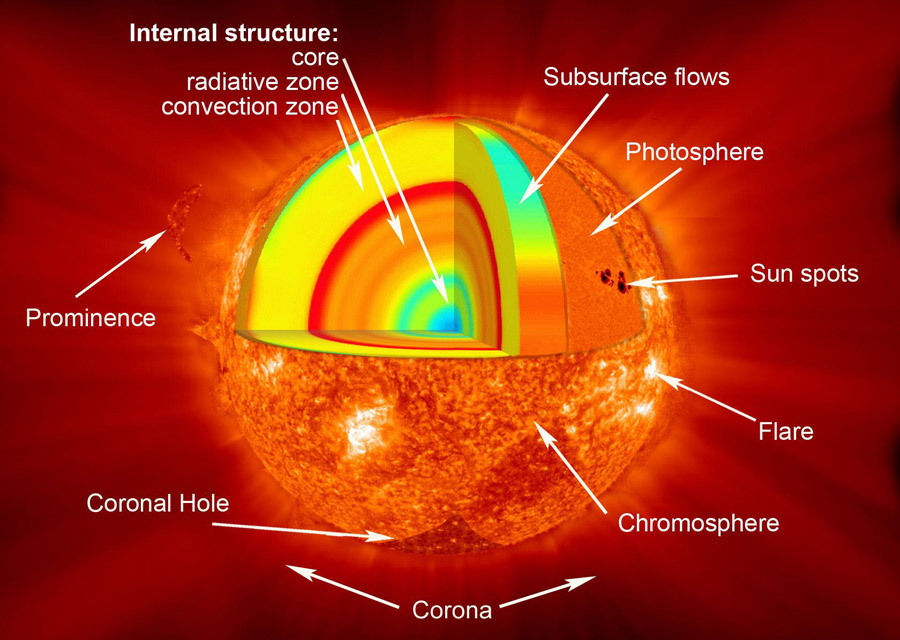
La radiación solar puede ser estimada como un cuerpo negro a temperatura \(T_\mathrm{sun} = 5777 K\). Sin embargo, la radiación solar es el resultado de la emisión de muchas capas con diferente composición, y cuya temperatura puede alcanzar más de 100,000 K.

../_images/sun_structure.png

7.2.1. Constante solar#

Consideremos el sol como un cuerpo negro a temperatura \(T_\mathrm{sun} = 5777\) K.

El calor total por radiación emitido por el sol es \(\pi D_\mathrm{sun}^2 E_\mathrm{sun}\), donde \(D_\mathrm{sun} = 1.39\times 10^9\) m es el diámetro del sol.

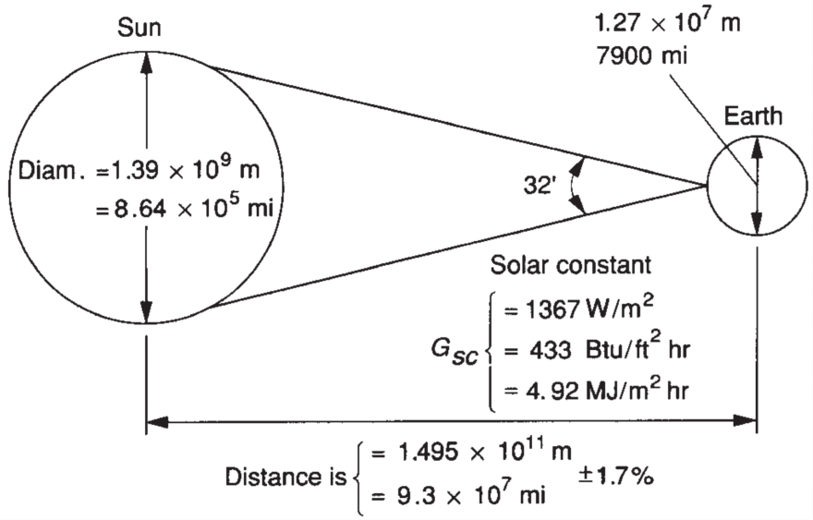
Considerando la distancia entre el sol y la tierra, \(d_\mathrm{e-s} = 1.495\times 10^{11}\) m, el flujo de radiación sobre la superficie de la tierra, \(G_\mathrm{sc}\), es:

(7.2)#\[\begin{equation} G_\mathrm{sc} = \sigma T_\mathrm{sun}^4 \frac{\pi D_\mathrm{sun}^2}{4\pi d_\mathrm{e-s}^2}=1367\frac{\mathrm{W}}{\mathrm{m}^2} \end{equation}\]

La constante solar \(G_\mathrm{sc} = 1367\) W/m\(^2\) es el flujo de energía sobre una superficie perpendicular a los rayos solares y a la distancia media entre la tierra y el sol. En otras palabras, corresponde radiación extraterrestre del sol que incide sobre 1 m\(^2\) en la tierra.

../_images/solar_constant.png

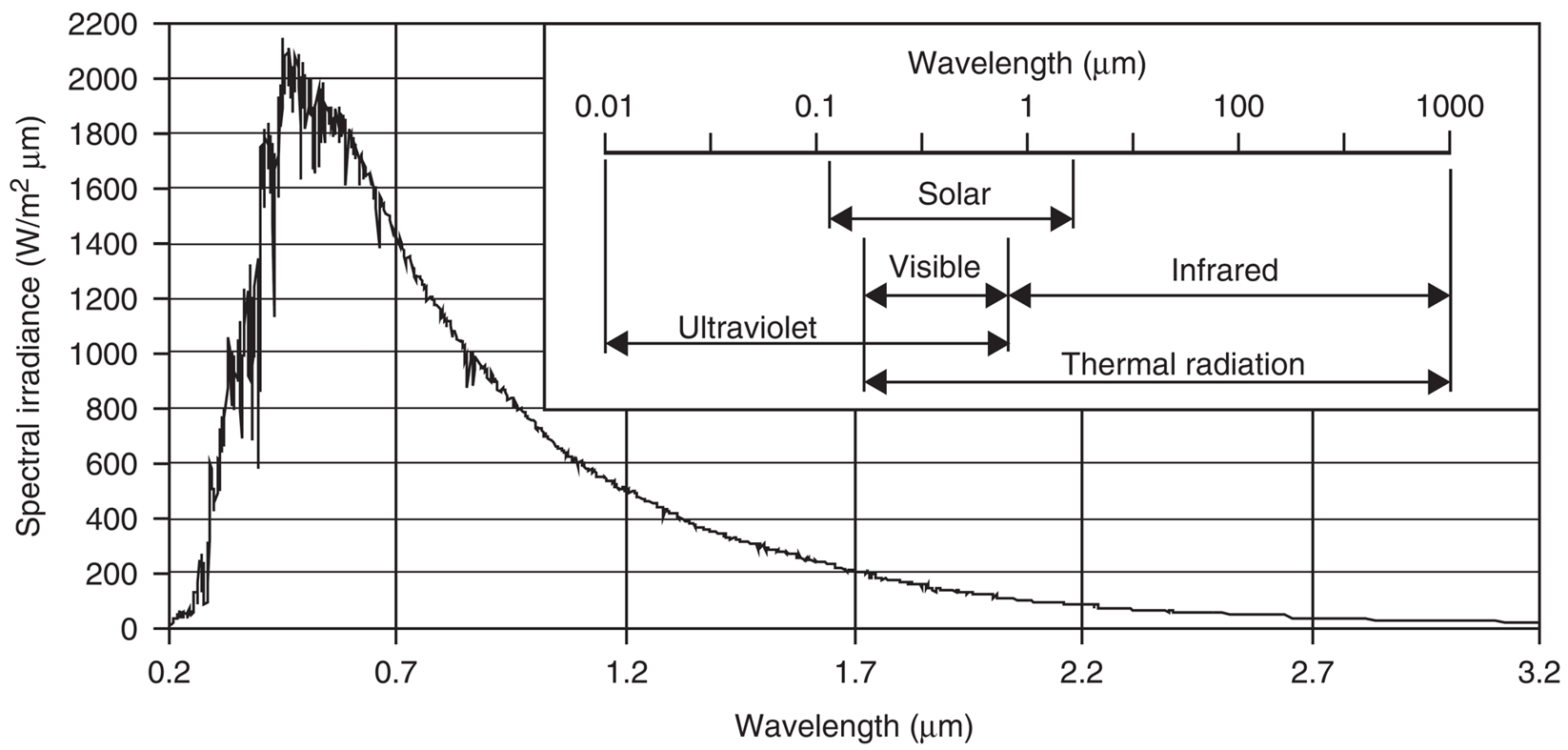
La siguiente figura ilustra la variación espectral de la constante solar, según reportado en la norma ASTM E-490

../_images/extraterrestial_solar_radiation.png

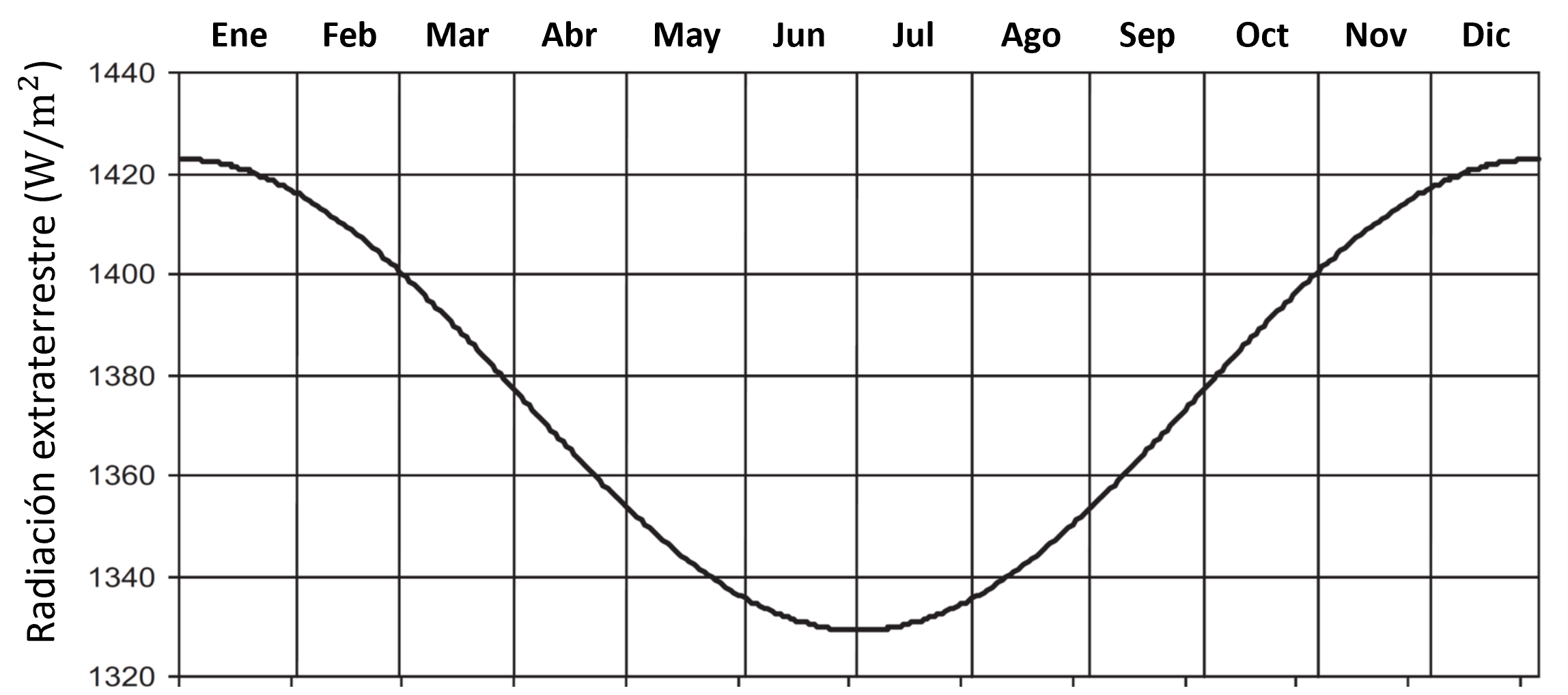
Debido a la excentricidad de la órbita de la tierra, la constante solar varía alrededor de un 3.3% largo del año. Para un día \(N\) de un total de 365, la constante solar está dada por:

(7.3)#\[\begin{equation} G_\mathrm{sc,N} = G_\mathrm{sc}\left[1+0.033\cos\left(\frac{360N}{365}\right)\right] \end{equation}\]
../_images/solar_constant_daily.png

La constante solar también cambia según la elevación solar o, de forma complementaria, con el cenit solar en la forma:

(7.4)#\[\begin{equation} G_{\mathrm{sc},t} = G_\mathrm{sc}\cos\theta_\mathrm{s} \end{equation}\]

Para una superficie inclinada, con un ángulo de incidencia \(\theta_i\) la constate solar es:

(7.5)#\[\begin{equation} G_{\mathrm{sc},s} = G_\mathrm{sc}\cos\theta_\mathrm{i} \end{equation}\]

7.2.2. Atenuación atmosférica#

La radiación solar definida por \(G_\mathrm{sc}\) corresponde al valor fuera de la atmosfera de la tierra. En la superficie de la tierra, este valor es atenuado debido a fenómenos de absoción y scattering asociado a los gases atmosfpericos, tales como vapor de agua, ozono, nubes, etc.

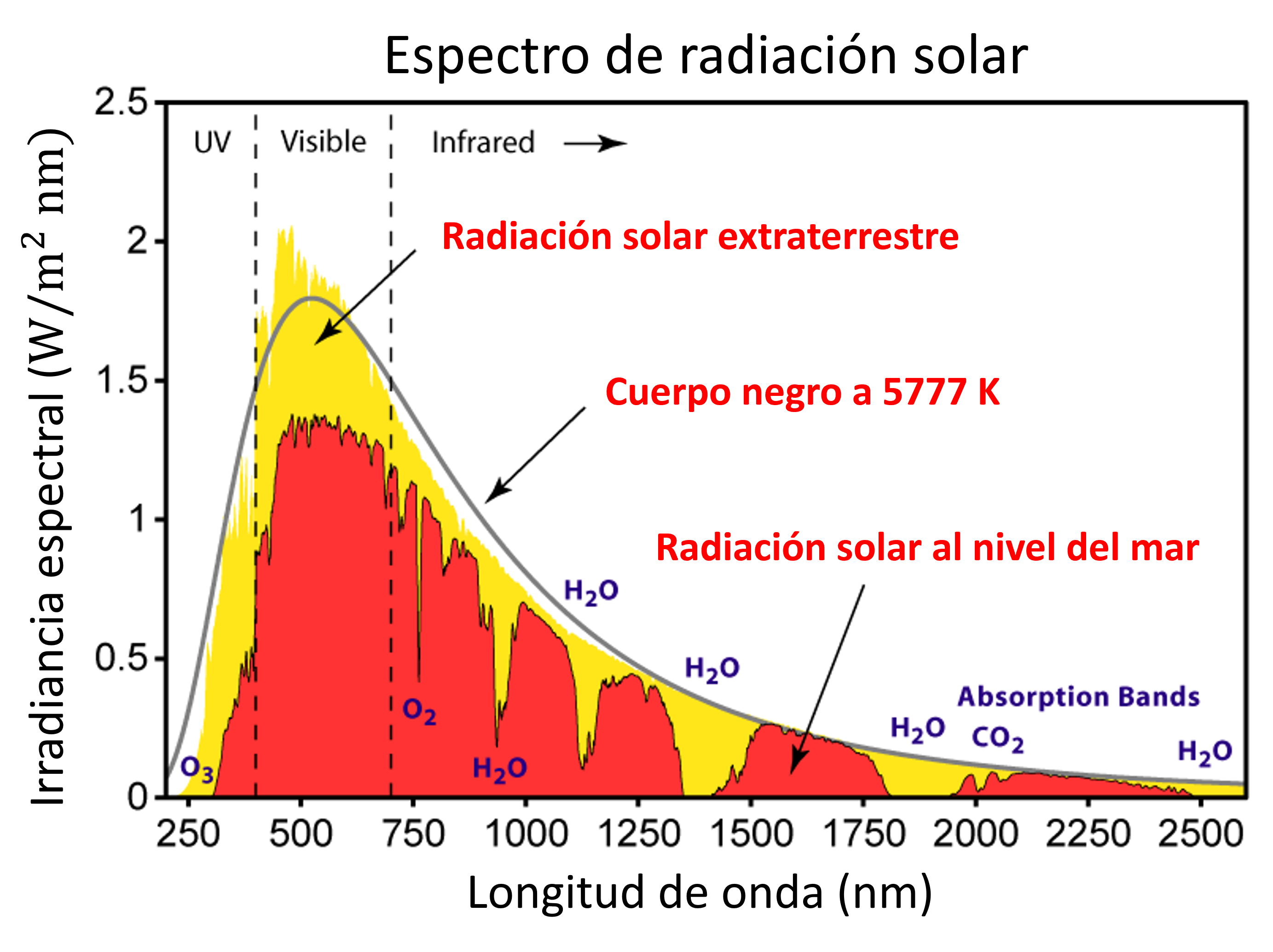
../_images/Solar_Spectrum_atmosphere.png

En general esta atenuación dependen de la ángulo de elevación del sol y, por lo tanto varía según el día del año y la latitud en la que se encuentra el observador

Definimos como coeficiente de masa de aire (\(\mathrm{AM}\)) como:

\[\begin{equation*} \mathrm{AM} = \frac{L}{L_0} \end{equation*}\]

donde \(L_0\) es la distancia (espesor de la atmósfera) normal a la superficie de la tierra y al nivel del mar, y \(L\) es la distancia al nivel del mar a un ángulo \(\theta_\mathrm{s}\)

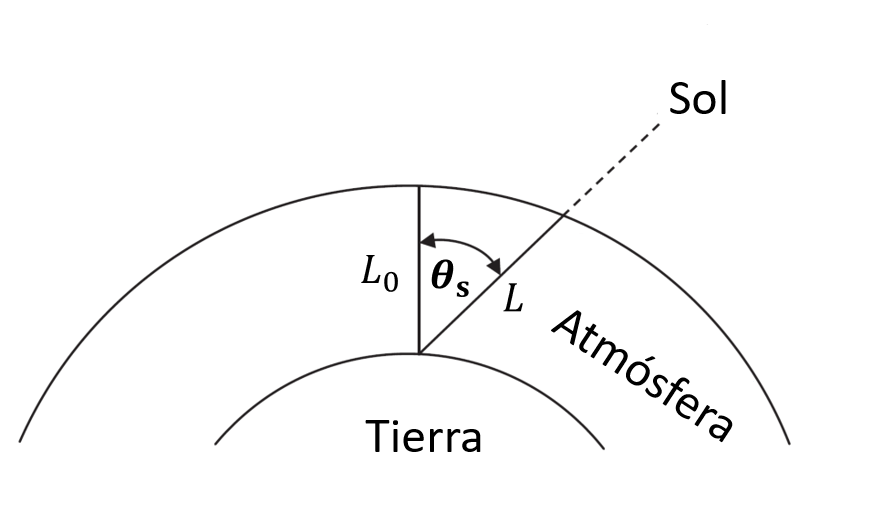
../_images/AM_diagram.png

Una forma simplificada de representar el coeficiente de masa de aire es:

(7.6)#\[\begin{equation} \mathrm{AM} = \frac{1}{\cos\theta_\mathrm{s}} \end{equation}\]

  • \(\mathrm{AM}0\) corresponde al espectro de radiación solar extraterrestre.

  • \(\mathrm{AM}1\) corresponde al espectro de radiación a nivel del mar con el sol en dirección normal a la superficie.

  • \(\mathrm{AM}1.5\) corresponde al espectro de radiación a nivel del mar con el sol \(\theta_\mathrm{s} = 48.19\)°

El coeficiente de masa de aire \(\mathrm{AM}1.5\) representa una aproximación del promedio general anual de radiación solar en latitudes correrspondiente a regiones como Japón, China, Estados Unidos y Europa. Así, este valor se ha convertido en el estandar para caracterizar el desempeño de tecnologías de energía solar.

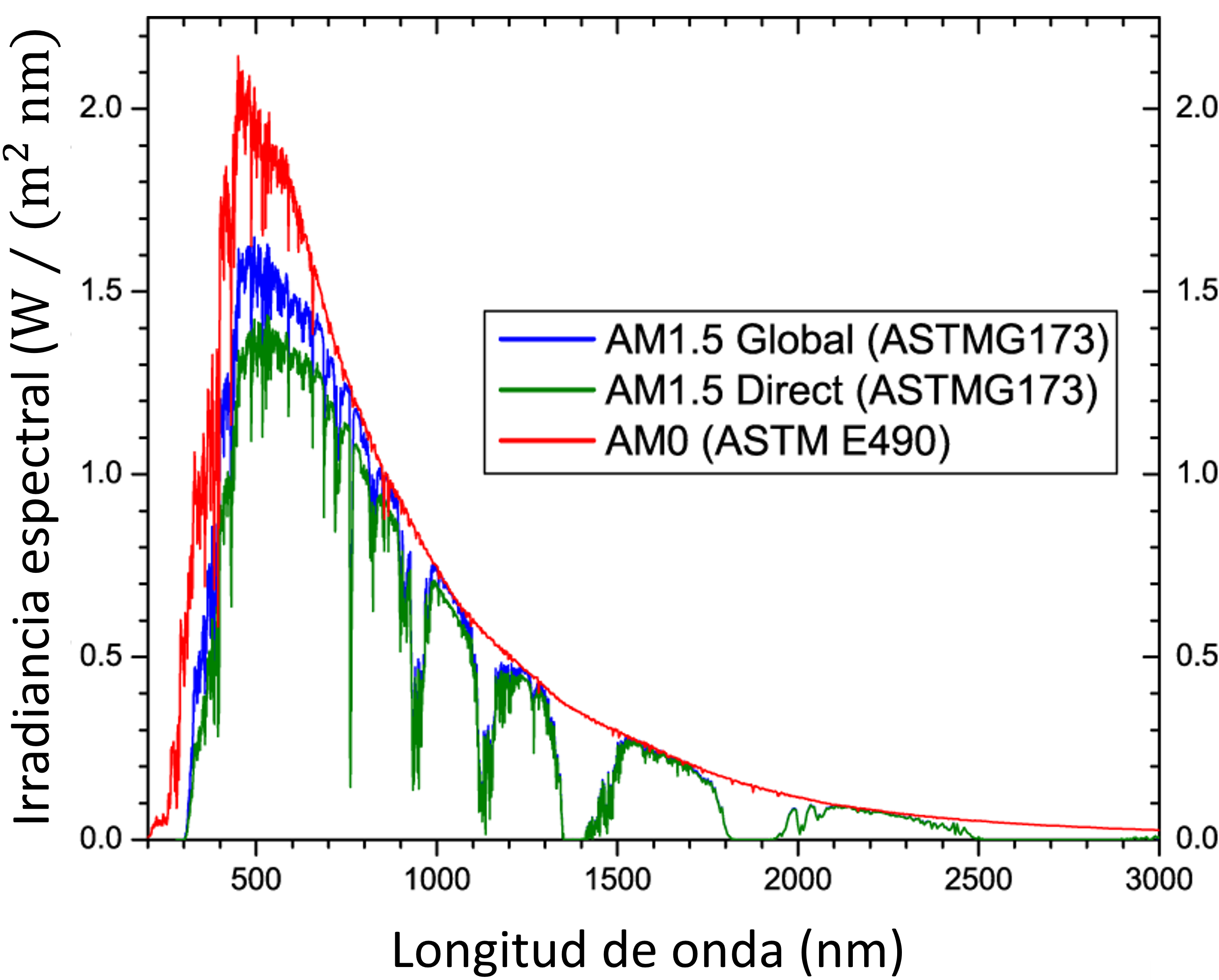
../_images/am1.5.png

Debido al scattering atmosférico, el espectro \(\mathrm{AM}1.5\) considera una componente global (directa + difusa) y una directa.

La irradiancia hemisférica total del espectro \(\mathrm{AM}1.5\), es

(7.7)#\[\begin{equation} G_\mathrm{AM1.5} = 1000~\frac{\mathrm{W}}{\mathrm{m}^2} = 1~\mathrm{sun} \end{equation}\]

Existen distintas fuentes con valores tabulados del espectro AM1.5, por ejemplo: NREL AM1.5

7.3. Componentes de la radiación solar#

La radiación solar no esta compuesta únicamente de un haz de rayos especulares. Si así fuera, no tendríamos visibilidad al bloquear el sol con nuestras manos.

En efecto, la radiación solar está compuesta por una série de componentes.

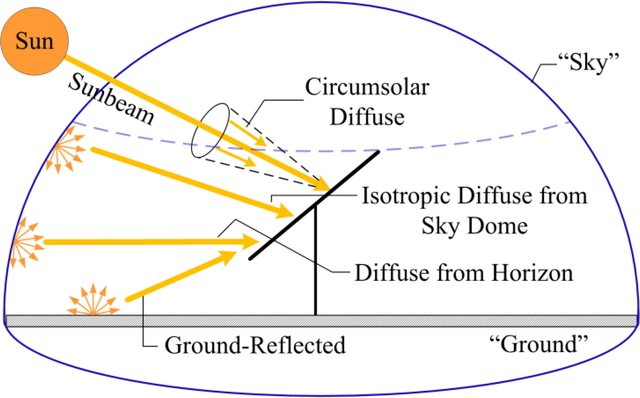
../_images/solar_components.jpg

Tal como indica la figura, las componentes de la radiación son:

  • Directa (beam): Correspondiente a los rayos speculares del sol.

  • Difusa circumsolar: Asociada al scattering hacia adelante alrededor del disco solar.

  • Isotrópica difusa: Asociada a la componente uniforme (isotrópica) del scattering producida alrededor del domo del cielo.

  • Difusa del horizonte: Corresponde a la componente del scattering en el plano del horizonte, la cual es más intensa que la componente isotrópica difusa.

  • Terrestre reflejada o albedo (ground): radiación reflejada por el suelo.

Comúnmente, las mediciones de radiación solar se reportan usando tres parámetros de irradiancia (radiación sobre una superficie):

  • Irradiancia normal directa (Direct Normal Irradiance o DNI): Corresponde a la radiación sobre una superficie apuntando en dirección normal a los rayos del sol. Considera la componente directa y circumsolar de la radiación solar.

  • Irradiancia horizontal difusa (Diffuse Horizontal Irradiance o DHI): Corresponde a la radiación isotrópica difusa y difusa del horizonte que incide sobre una superficie horizontal.

  • Irradiancia horizontal global (Global Horizontal Irradiance o GHI). Corresponde a \(\mathrm{GHI} = \mathrm{DNI}\cos\theta_i + \mathrm{DHI}\)

7.4. Instrumentos de medición de radiación solar#

Para diseñar sistemas basados en energía solar, es necesario caracterizar una serie de parámetros de la radiación solar. Estos incluyen, irradiación solar hemisférica, especular y difusa.

En general, los instrumentos de medición se basan en sensores termoeléctricos o fotovoltaicos, que permiten medir el flujo de energía y no la componente espectral. La irradiancia espectral, generalmente se obtiene por modelos de transporte radiativo.

Existen dos tipos de instrumentos para medir la irradiancia solar: el piranómetro y el pirheliómetro.

7.4.1. Piranómetro#

Este instrumento mide la componente GHI

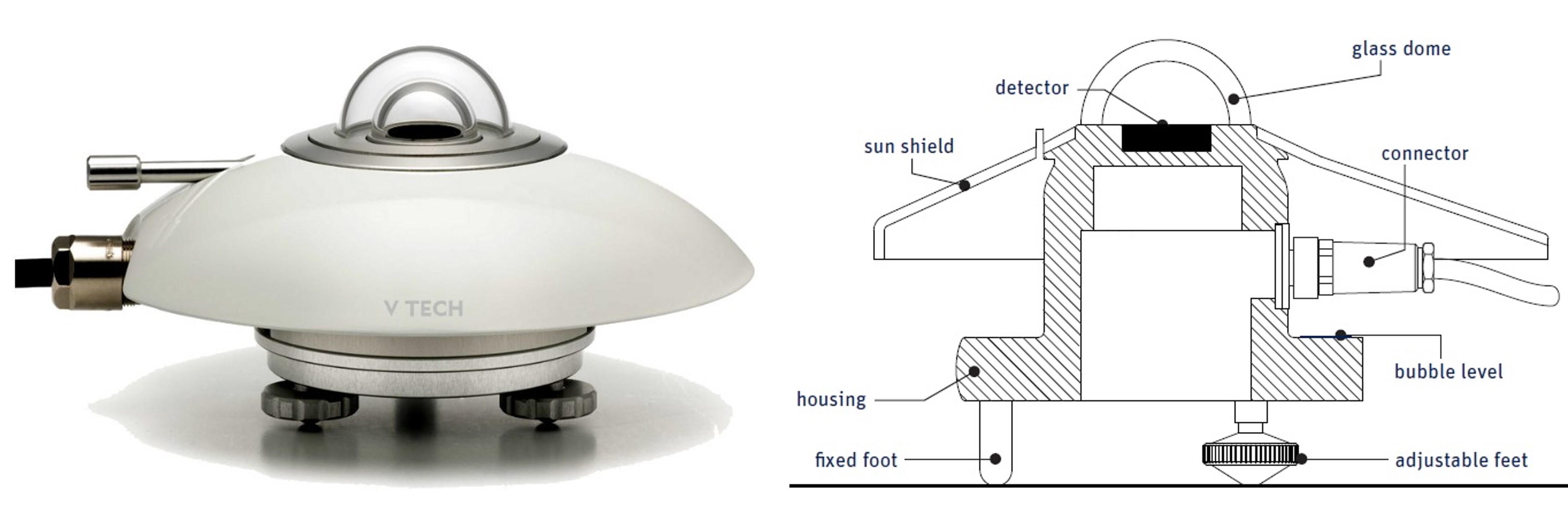
../_images/pyranometer.jpg

Esta compuesto de un domo superior (glass dome) conformado por dos cámaras de vidrio, donde el aire atrapado actúa como aislante térmico. Al interior del domo se ubica un detector que absorbe la radiación solar. El cambio de temperatura del absorbedor es correlacionado con el flujo de calor por radiación. El detector está rodado de una cubierta aislante (housing) y un escudo de radiación solar (sun shield) para evitar ganancias parasíticas de calor.

El piranómetro también puede ser utilizado para medir la componente DHI. En este caso se utiliza una banda que bloquea la componente directa y circumsolar.

../_images/pyranometer_diffuse.png

7.4.2. Pirheliómetro#

Este instrumento permite medir la componente DNI de la radiación solar.

../_images/pyrheliometer.jpg

7.5. Mapas solares#

Existen diversos mapas solares disponibles en línea. En general, estos reportan valores de GHI, DNI y DHI medidos a lo largo de un año.

Los más recomendados son:

  • Explorador solar del ministerio de energía. Entrega información detallada de las componentes DNI, DHI y GHI por més y año en el territorio chileno. La herramienta permite exportar los datos en formato .csv con información detallada de irradiancia directa y difusa para superficies orientadas en distintos ángulos. Además, permite estimar el desempeño de un colector solar y paneles fotovoltaicos.

  • Global Solar Atlas, del World Bank Group. Corresponde a un mapa global de la radiación solar, con reportes de DNI, DHI y GHI anuales, y reportes detallados del DNI distribuido por mes y día. Además permite estimar el desempeño de paneles fotolvaicos por kWp (kiloWatt peak) a través del parámetro PVOUT.

Es importante mencionar que la componente DNI no siembre es dominante.

Coordenadas

Localidad

DNI
(kWh/m\(^2\)-año)

GHI
(kWh/m\(^2\)-año)

DHI
(kWh/m\(^2\)-año)

-45.51°, -73.52°

Aysén

848.2

1025.9

556.2

-23.92°, -69.49°

Antofagasta

3330.4

2604

575

En el caso de la región de Asyén, la componente normal de la irradiancia sobre una superficie horizontal, es GHI - DHI = 468.7 kW/m\(^2\) - año (aproximadamente 45.7% del GHI), mientras que en Antofagasta es, 2029.0 kW/m\(^2\) - año (aproximadamente 77.9% del GHI).

Notar, además, que en ninguno de los dos ejemplos el valor GHI - DHI coincide con el DNI. Esto debido a que la primera considera el factor \(\cos\theta_i\) asociado al ángulo de incidencia.

7.6. Referencias#

  • Kalogirou S. A. Chapter 2: Environmental Characteristics en Solar Energy Engineering Processes and Systems, 2nd Ed, Academic Press, 2014

  • Duffie J. A., Beckman W. A. and Blair N. Chapter 1: Solar Radiation and Chapter 2: Available Solar Radiation en Solar Engineering of Thermal Processes, 5th Ed, Jhon Wiley and Sons, 2020

Contents