9. Problemas de valor inicial#
9.1. Introducción#
Las ecuaciones diferenciales son utilizadas para modelar sistemas en todos los campos de ciencia e ingeniería.
Como definición general, un sistema de ecuaciones diferenciales define la relación entre:
variables dependientes, \(f_1(x_1,x_2, \cdots)\), \(f_2(x_1,x_2, \cdots), \cdots\)
las variables independientes \(x_1,x_2,x_3, \cdots\), y
sus derivadas.
9.1.1. Clasificación de ecuaciones diferenciales#
Una ecuacion diferencial puede estar compuesta por una variable dependiente y una independiente.
Por ejemplo, la ecuación del péndulo que define la variación temporal del ángulo \(\Theta\) en función del tiempo \(t\):
donde \(g\) es la gravedad, \(m\) la masa del péndulo, \(l\) es la distancia al centro de rotación y \(\kappa\) es una constante a amortiguación asociado al arrastre por el viento
Este tipo de ecuaciones se conoce como ecuación diferencial ordinaria (EDO), debido a que la varible dependiente (\(\Theta\), en este caso) está condicionada por una variable independiente (\(t\), en este caso). Debido al término \(\sin\Theta\), esta ecuación corresponde a una EDO no-lineal.
Si el ángulo de oscilación, \(\Theta\), es pequeño, podemos hacer la simplificación \(\sin \Theta\approx \Theta\).
En este caso la ecuación se transforma en una EDO lineal:
En general, las EDO lineales tiene solución analítica.
También podemos tener una ecuación diferencial definida para una variable dependiente y multiples variables independientes.
Un buen ejemplo es la ecuación de difusión de calor, que describe la distribución de temperatura en función del tiempo, \(t\), y el espacio. En el caso 2D:
donde \(\rho\) es la densidad, \(c_p\) es el calor específico, y \(k\) es la conductividad térmica
Este tipo de ecuacion, con más de una variable independiente, se conocen como ecuación diferencial parcial (EDP)
En este caso, la EDP es del tipo lineal
Por último, en el caso de más de una variable dependiente, podemos tener sistemas de ecuaciones diferenciales del tipo EDO o EDP.
Tal es el caso de la ecuación de Navier-Stokes utilizada en mecánica de fluidos para modelar un problema en dos dimenciones:
En este caso tenemos un sistema de 3 EDPs no-lineales definido para tres variables dependientes (\(u\), \(v\), y \(p\)) en función de tres variables independientes (tiempo \(t\) y el espacio \(x\) e \(y\)). Donde \(u(t,x,y)\) y \(v(t,x,y)\) son, respectivamente, el campo de velocidad en dirección \(\hat{x}\) y \(\hat{y}\); y \(p(t,x,y)\) es el campo de presiones. Nuevamente, \(\rho\), es la densidad del fluido.
También podemos clasificar una ecuación diferencial según el orden de sus derivadas.
Por ejemplo, la ecuación:
Es una EDO de segundo orden, debido a que \(\Theta\) es derivada dos veces respecto a \(t\).
9.1.2. Condiciones de borde y condiciones iniciales#
Las ecuaciones diferenciales presentadas anteriormente representan una formulación general asociada a un fenómeno físco (movimiento de un péndulo, distribución de temperaturas o movimiento de un fluido). Sin embargo, estas ecuaciones no están condicionadas a un problema en específico y, por lo tanto, su solución es definida en base a constantes de valor arbitrario.
Por ejemplo, la versión lineal de la EDO del péndulo tiene como solución general:
Para asociar una ecuacion diferencial a un problema específico necesitamos condiciones de borde o condiciones iniciales
9.1.2.1. Condiciones iniciales#
Usamos condiciones iniciales si la variable dependiente evoluciona respecto a la variable independiente.
Por ejemplo, en el caso del péndulo, el ángulo \(\Theta\) evoluciona respecto al tiempo, \(t\), y por lo tanto necesitamos de condiciones inciales.
Como condición inicial, por ejemplo, asumamos que el péndulo está en reposo con un ángulo \(\Theta_0\):
Ecuación gobernante
Condiciones iniciales
Nota El número de condiciones iniciales debe ser igual al número de derivadas de la variable independiente.
Comúnmente, las condiciones iniciales están asociadas a la variable tiempo. Sin embargo, una condición inicial también puede estar asociada a una variable espacial.
Por ejemplo, la ecuación que describe el cambio de temperatura del agua (\(T_f\)) a lo largo del eje axial (\(y\)) de los tubos de un colector solar está dado por:
Ecuación gobernante
Condición de borde
donde \(T_{f,i}\) es la temperatura del agua a la entrada del colector, \(\dot{m}\) es el flujo másico de agua por el colector, \(T_a\) es la temperatura ambiente, \(S\) es la radiación solar absorbida, \(c_p\) es el calor específico del agua, \(U_L\) es el coeficiente global de transferencia de calor, y \(n\), \(W\) y \(F'\) son parámetros de diseño del colector.
En este caso, la temperatura del agua (\(T_f\)) evoluciona al recorrer el eje axial de los tubos. Así, este problema también podría ser considerado como un problema con valor inicial.
9.1.2.2. Condiciones de borde#
Usamos condiciones de borde si la variable dependiente está determinada en más de un valor de la variable independiente.
Por ejemplo, la distribución de temperaturas de una placa cuadrada de largo \(L\), incialmente a temperatura \(T_a\), con temperaturas en \(T_h\) y \(T_c\) en los bordes izquierdo y derecho, y tempertura \(T_0\) en la parte superior e inferior, está descrita por la ecuación:
Ecuación gobernante
Condiciones de borde
condición inicial
El número de condiciones de borde debe ser igual al número de derivadas respecto a la variable independiente
Las condiciones de borde están, generalmente, asociadas a variables en el espacio
9.2. Aspectos generales de los métodos numéricos para solución de EDOs#
9.2.1. Ecuación diferencial ordinaria (EDO) con valor inicial#
En forma general, podemos representar una EDO con valor inicial de la forma:
sujeta a las condiciones inciales: \(t = 0, f(0), f^{(1)}(0), f^{(2)}(0),\ldots, f^{(n)}(0)\)
Por ejemplo, en el caso de la ecuación del péndulo:
donde \( F(t,\Theta, \dot{\Theta}) = - \frac{g}{l}\sin \Theta - \frac{\kappa}{ml}\dot{\Theta} \)
Convenientemente, podemos reescribir esta ecuación como:
que en su forma matricial se reduce a
con condición inicial
A partir de este procedimiento, hemos reducido una EDO de orden superior a una EDO de primer orden de la forma:
con una condición inicial \(\vec{y}(0)\).
donde
Como cololario general, tenemos que siempre podemos transformar una EDO de orden superior a un sistema de EDOs de primer orden
Esto nos permite enfocarnos en métodos numéricos para resolver una EDO (o un sistema de EDOs) de primer orden.
9.2.2. Método de Euler explícito#
Dada la condición inicial \(\vec{y}(t_0)\), supongamos que queremos determinar el valor de \(\vec{y}\) en un tiempo \(t_0 +\Delta t\).
La forma más sencilla es mediante una expansión de Taylor centrada en \(t_0\):
Truncando los términos de segundo y mayor orden tenemos:
Podemos seguir repetiendo este procedimiento para encontrar la evolución \(\vec{y}\) en el tiempo.
En su forma general, este método se conoce como el método de Euler explícito:
donde \(\vec{y}_{i+1} = \vec{y}(t_i + \Delta t)\), y \(h = \Delta t\)
Gráficamente, el método consiste en aproximar el valor de \(\vec{y}_{i+1}\) mediante una recta en el punto \(t_i, \vec{y}_i\), cuya pendiente es \(\vec{F}[t_i,\vec{y}_i]\)
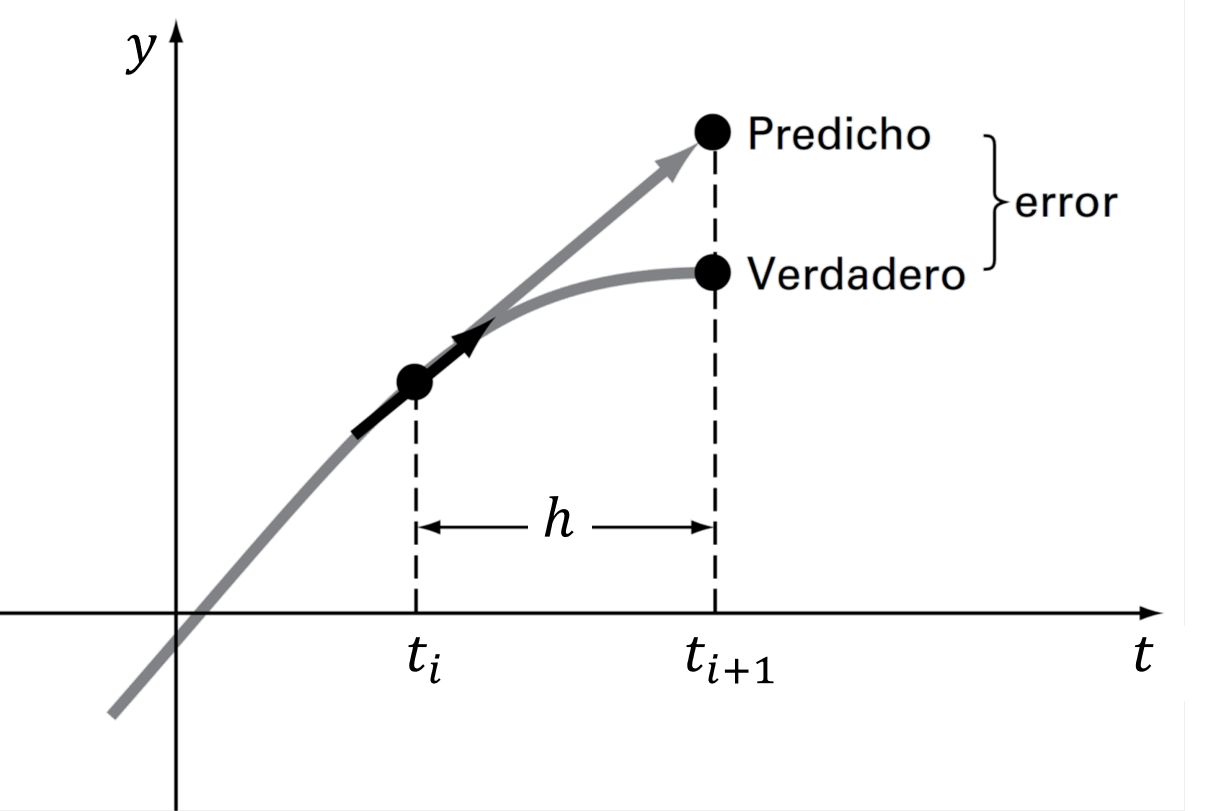
Por ejemplo, consideremos la ecuación diferencial:
con condición inicial \(y(0) = -0.5\)
Utilicemos el método de Euler para resolver este problema en el intervalo \(t\in[0,1]\) con \(h = 0.1\) y \(h = 0.01\). Compararemos nuestra solución con la solución exacta \(y(t) = -\frac{1}{2}e^{-2t}\).
import numpy as np
# Solución exacta
y_exact = lambda t: -0.5*np.exp(-2*t)
# Definimos parámetros numéricos
h = 0.1 # paso de tiempo (dt)
t0, tf = 0, 1 # tiempo inicial (ti) y final (tf)
t = np.arange(t0, tf+h, h) # lista de tiempos
# Escribimos ecuación diferencial en formato de código
F = lambda t, y: np.exp(-2*t) # Ecuación gobernante dy = F(t,y)
y0 = -0.5 # Condición inicial
# Método de Euler
y = np.zeros(len(t)) # arreglo vacio para y
y[0] = y0
for i in range(len(t)-1):
y[i+1] = y[i] + h*F(t[i], y[i]) # Euler explicito
import matplotlib.pyplot as plt
plt.figure(figsize = (4, 3))
plt.rcParams.update({'font.size': 10}) # Tamaño de fuente
# arreglo de tiempos para graficar sol exacta
t_plot = np.linspace(t0, tf, 100)
plt.plot(t, y, 'ro--', label='Euler')
plt.plot(t_plot, y_exact(t_plot), 'k', label='Solución exacta')
plt.title(r'Evaluación ecuación $\frac{dy}{dt} = e^{-2t}; y(0) = -0.5$')
plt.xlabel('t')
plt.ylabel('y(t)')
plt.grid()
plt.legend(loc='lower right')
plt.show()
9.2.3. Precisión#
En el ejemplo anterior, notamos una considerable mejora en la aproximación cuando disminumos \(h\), de \(h = 0.1\) a \(h = 0.01\). Esto es una consecuencia directa del error de truncamiento \(O(h^2)\).
Por otro lado, en ambos casos notamos que el error aumenta a medida que nos alejamos del valor inicial. Esta propagación del error ocurre porque el error de truncamiento nos entrega una estimación del error local, es decir, durante un solo paso del método.
En base a esto, caracterizamos la presición de un método considerando dos tipos de error:
Error de truncamiento local: Error del método para predecir la siguiente iteración (es decir, \(i\rightarrow i+1\)). Este error está asociado al truncamiento de la serie de Taylor.
Error de truncamiento global: Error por acumulación de errores de truncamiento local a lo largo de toda la iteración.
9.2.4. Estabilidad#
Otro término relevante en los métodos de solución de EDOs es la estabilidad. A diferencia de la precisión, que depende solo del método numérico escogido, la estabilidad depende de la EDO a resolver y del método escogido.
Es decir, un método puede ser estable para algunos problemas e inestable para otros.
Analicemos el problema de estabilidad con la siguiente EDO:
con condición inicial \(y(0) = 0.5\)
Utilicemos el método de Euler para encontrar la solución en el intervalo \(t\in[0,1]\) con \(h = 0.09\) y \(h = 0.01\). Compararemos nuestra solución con la solución exacta \(y(t) = 0.5e^{-20t}\).
import numpy as np
# Solución exacta
y_exact = lambda t: 0.5*np.exp(-20*t)
# Definimos parámetros numéricos
h = 0.09 # paso de tiempo
t0, tf = 0, 1 # tiempo inicial (ti) y final (tf)
t = np.arange(t0, tf+h, h) # lista de tiempos
# Ecuación diferencial
F = lambda t, y: -20*y # Ecuación gobernante dy = F(t,y)
y0 = 0.5 # Condición inicial
# Método de Euler
y = np.zeros(len(t))
y[0] = y0
for i in range(len(t)-1):
y[i+1] = y[i] + h*F(t[i], y[i])
import matplotlib.pyplot as plt
plt.figure(figsize = (6, 4))
plt.rcParams.update({'font.size': 10}) # Tamaño de fuente
# arreglo de tiempos para graficar sol exacta
t_plot = np.linspace(t0, tf, 100)
plt.plot(t, y, 'ro--', label='Euler')
plt.plot(t_plot, y_exact(t_plot), 'k', label='Solución exacta')
plt.title(r'Evaluación ecuación $\frac{dy}{dt} = e^{-2t}; y(0) = -0.5$')
plt.xlabel('t')
plt.ylabel('y(t)')
plt.grid()
plt.legend(loc='lower right')
plt.show()
Observamos que el método de Euler converge cuando \(h = 0.01\), pero oscila constantemente para \(h > 0.1\). Esta es un característica típica de un problema de estabilidad.
En otras palabras, el método de Euler explícito es condicionalmente estable
Es posible demostrar que para ecuaciones del tipo \(\frac{dy}{dt} = -ay\), la condición de estabilidad del método de Euler explícito está dada por \(h > 2/a\).
Sin embargo, no existe una regla universal para identificar las condiciones de inestabilidad y, en general, depende del tipo de ecuación diferencial, el método a utilizar, y el paso de tiempo \(\Delta t = h\).
9.2.5. Método de Euler implícito#
Alternativamente, podemos definir el argumento de \(\vec{F}(t,\vec{y})\) en función de los valores futuros \(t_{i+1}\) y \(\vec{y}_{i+1}\):
Esta formulación se define como implícita debido a que el valor futuro, \(\vec{y}_{i+1}\) se encuentra a ambos lados de la ecuación.
Así, llamamos a este algoritmo Método de Euler implícito.
Si bien, esta formulación también tiene un error de truncamiento \(O(h^2)\), es más estable que Euler explícito (lo veremos con un ejemplo).
Notar que la formulación implícita da lugar a valores desconocidos, \(y_{i+1}\), al lado derecho de la ecuación. Esto implica que, para cada iteración debemos resolver un sistema de ecuaciones para encontrar \(\vec{y}_{i+1}\).
Debido a que, en general, el sistema de ecuaciones que encontraremos es no lineal, debemos utilizar un método de solución de raices para encontrar \(\vec{y}_{i+1}\) (por ejemplo, Newton-Raphson).
En otras palabras, dado un tiempo inicial \(t_0\) y condiciones iniciales \(\vec{y}_0\), el valor de \(\vec{y}_1\) está dado por las raices de:
Para encontrar el valor en el tiempo \(t_2, t_3, \dots,t_n\), repetimos el procedimiento anterior de forma iterativa, resolviendo la ecuación:
Revisemos esto con el ejemplo anterior, ahora usando Euler implícito.
import numpy as np
from scipy.optimize import fsolve
# Solución exacta
y_exact = lambda t: 0.5*np.exp(-20*t)
# Definimos parámetros numéricos
h = 0.1 # paso de tiempo
t0, tf = 0, 1 # tiempo inicial (ti) y final (tf)
t = np.arange(t0, tf+h, h) # lista de tiempos
# Ecuación diferencial
F = lambda t, y: -20*y # Ecuación gobernante dy = F(t,y)
y0 = 0.5 # Condición inicial
# Método de Euler
y = np.zeros(len(t)) # inicializamos arreglo para yi+1
y[0] = y0 # guardamos condicion inicial
for i in range(len(t)-1): # itereamos según paso de tiempo
# Guardamos valores conocidos
ti, ti1, yi = t[i], t[i+1], y[i]
# Definimos la función objetivo para la búsqueda de raices
E_implicit = lambda yi1: yi1 - (yi + h*F(ti1, yi1))
# Buscamos la raiz de forma iterativa con valor inicial y0
ysol = fsolve(E_implicit, x0 = yi)[0]
y[i+1] = ysol # Guardamos el valor para la siguiente iteración
import matplotlib.pyplot as plt
plt.figure(figsize = (6, 4))
plt.rcParams.update({'font.size': 10}) # Tamaño de fuente
# arreglo de tiempos para graficar sol exacta
t_plot = np.linspace(t0, tf, 100)
plt.plot(t, y, 'ro--', label='Euler implícito')
plt.plot(t_plot, y_exact(t_plot), 'k', label='Solución exacta')
plt.title(r'Evaluación ecuación $\frac{dy}{dt} = e^{-2t}; y(0) = -0.5$')
plt.xlabel('t')
plt.ylabel('y(t)')
plt.grid()
plt.legend()
plt.show()
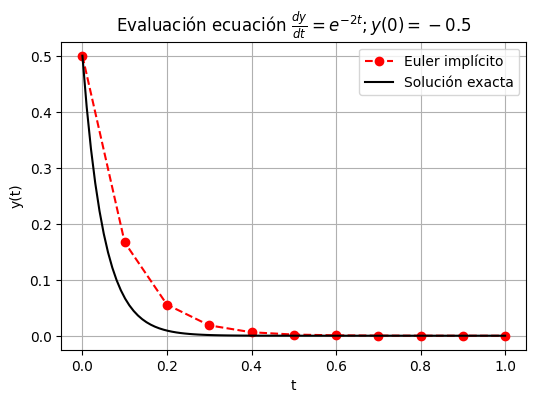
En el ejemplo vemos que, si bien la precisión sigue condicionada al error de truncamiento \(O(h^2)\), el método no presenta problemas de inestabilidad
En efecto, para ODEs de la forma \(\frac{dy}{dt} = -ay\), el métodod de Euler implícito es incondicionalmente estable.
En resumen, en la solución de una ODE debemos considerar la precisión y la estabilidad del problema. Si bien, la precisión está exclusivamente asociada al método, la estabilidad depende del método y la EDO a resolver.
En el ejemplo anterior fue posible cuantificar las condiciones de estabilidad debido a que la EDO era del tipo lineal. En general, no siempre es posible acotar la inestabilidad de forma analítica, especialmente para EDOs no lineales.
En la práctica, los términos precisión y estabilidad se confunden debido a que comúnmente ambos están asociados por \(h\). Sin embargo, cada uno es un aspecto independiente. Así, un método con poca precisión puede ser muy estable, y viceversa.
9.3. Métodos de paso simple (Runge-Kutta)#
Los métodos de Runge-Kutta (RK) permiten aumentar el número de términos de una serie de Taylor, sin la necesidad de calcular derivadas de mayor orden
Esto permite una mejor precisión, ya que el error de truncamiento local se reduce.
Existen muchas variaciones, todas asociadas a una aproximación de la forma:
donde \(\phi\) se conoce como función incremento, que representa una pendiente representativa del intervalo
En su forma general, la función incremento está dada por:
donde \(a_j\) son constantes, y los valores \(k_j\) son:
donde \(p_m\) y \(q_{m,n}\) son constantes.
Notar que los valores de \(k_j\) están definidos por recurrencia, es decir \(k_j\) depende de \(k_{j-1}, k_{j-2}, \cdots, k_{1}\)
Para obtener una formulación específica debemos especificar \(n\).
Una vez definido el valor de \(n\), debemos igualar la expresión \(y_{i+1} = y_i + \phi h\) con los \(n\) términos de la expansión de Taylor:
A partir de esta igualdad generamos el número de ecuaciones necesarias para determinar \(a_j\), \(p_m\) y \(q_{m,n}\). Para más información, revisar el desarrollo para \(n = 2\) acá.
Lo importante de esta formulación es notar que el número de parámetros \(k_n\) tendrá asociado un error local \(O(h^{n+1})\), debido al truncamiento de la série de Taylor.
Así, por ejemplo, la formulación para \(n = 1\) permite aproximar hasta la primera derivada de la serie de Taylor. El fórmula resultante, que corresponde a RK1, es el método de Euler explícito que tiene un error de truncamiento local \(O(h^2)\).
Igualmente, un RK2, que corresponde a \(n=2\) (\(\phi = a_1k_1 + a_2k_2\)), tendría un error del orden \(O(h^3)\).
9.3.1. Runge-Kutta de segundo orden (RK2)#
La versión de segundo orden de RK es:
donde:
y las constantes \(a_1\), \(a_2\), \(p_1\) y \(q_{11}\), están dadas por:
Debido a que tenemos 3 ecuaciones y 4 incognitas, se debe acotar una de las variables para resolver el sistema
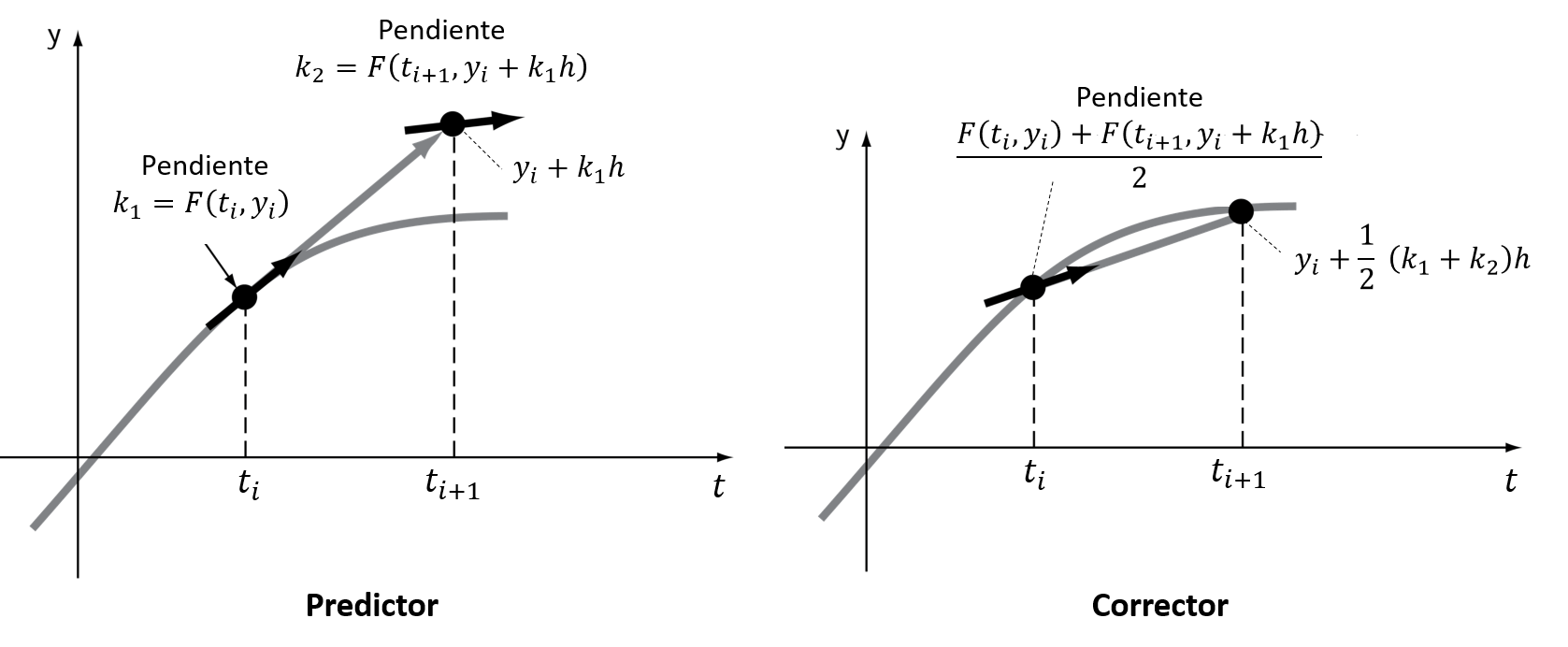
Esto da lugar a distintas versiones para RK2. Acá destacamos 2 (hay más versiones), que se conocen como métodos del tipo predictor-corrector.
Método de Heun (\(a_2 = 1/2\))
Método del punto medio (\(a_2 = 1\))
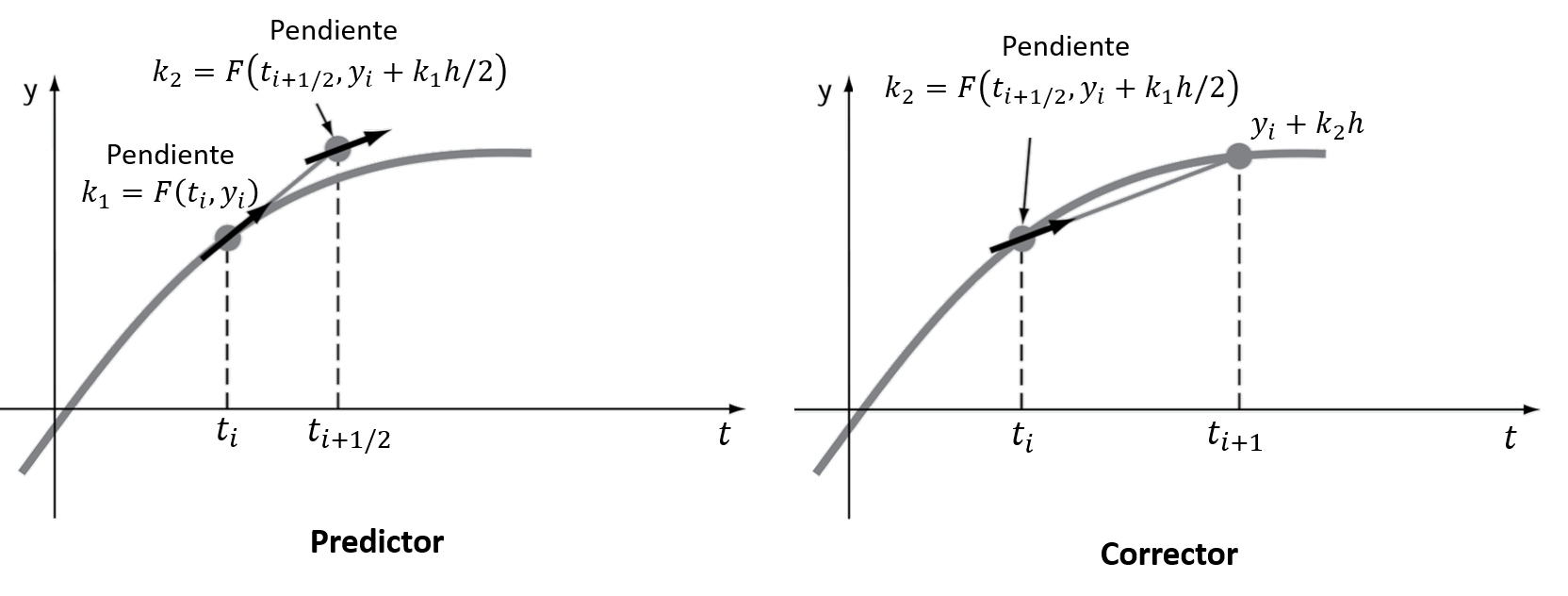
9.3.2. Runge-Kutta de cuarto orden (RK4)#
Los métodos RK de cuarto orden son los más populares. Al igual que con RK2, existen muchas versiones. La más popular es:
donde:
9.4. Métodos multipasos#
Los métodos discutidos hasta ahora se clasifican como métodos de paso simple debido a que el valor futuro \(y_{i+1}\) es determinado exclusivamente por la predicción anterior en el tiempo \(t_i\). Esto implica que los métodos no retienen la información para la predicción de aproximaciones en itereciones futuras (es decir, \(y_2\) considera el resultado en \(t_1\), pero no en \(t_0\)).
Este comportamiento hace que los métodos de paso simple sean ineficientes para problemas clasificados como rígidos, algo que discutiremos al final de esta unidad.
Los métodos multipasos, o de paso múltiple corrigen este comportamiento mediante polinomios de interpolación construidos a partir de una serie de estimaciones en tiempos previos, permitiendo mejorar la estimación de la trayectoria de la solución.
Esta característica, por otro lado, impica que los métodos multipasos demandan mayor capacidad de memoria que los métodos de paso simple.
Otra desventaja es que, debido a que los métodos multipaso requieren condiciones iniciales en varios pasos anteriores, se deben utilizar métodos alternativos (como de paso simple) para generar estos valores iniciales.
Los métodos más utilizados son los métodos de Adams-Bashforth, Adamns-Moulton y las fórmulas de diferenciación hacia atrás (BDFs). Esta última está implementada en la librería python oficial para resolver EDO con valor inicial.
9.5. Solución de EDOs en python (scipy.integrate.solve_ivp)#
En python, la función solve_ivp de la librería scipy.integrate permite resolver sistemas de EDOs con valor inicial.
Considerando los argumentos mínimos para llamar la función:
from scipy.integrate import solve_ipv
solve_ipv(fun,t_span, y0)
donde:
fun: (callable) función \(F(t,\vec{y})\)t_span = (ti, tf): (tupple) intervalo entre el valor inicial (ti) y final (tf).y0: (ndarray) condición inicial \(\vec{y}(0)\)
La función posee 5 métodos disponibles, los cuales se pueden condicionar con un cuarto argumento method.
Entre los métodos disponibles tenemos:
method = 'RK45': Runge-Kutta 4(5) explícito.method = 'RK23': Runge-Kutta 2(3) explícito.method = 'DOP853': Runge-Kutta 8 explícito.method = 'Radau': Runge-Kutta implícito de orden 5, conocido como Randau IIA.method = 'BDF': Método multipaso implícito basado en derivadas hacia atrás.
Por defecto method=RK45
También, al igual que con las librerías anteriores, podemos condicionar la tolerancia respecto al error relativo (rtol) y absoluto (atol).
from scipy.integrate import solve_ipv
solve_ipv(fun,t_span, y0, rtol = 1E-8, atol = 1E-8) # error absoluto y relativo menor a 1E-8
Por defecto, rtol = 1E-3 y atol = 1E-6.
Por ejemplo, consideremos la ecuación del péndulo:
Ecuación gobernante
Condiciones iniciales
Primero debemos transformar la ecuación a la forma \(\frac{d\vec{y}}{dt} = F(t,\vec{y})\):
Ecuación gobernante
Condiciones iniciales
Utilizamos solve_ivp para resolver el sistema en el intervalo \(t\in[0,5]\) s. En este problema las constantes son \(m = 200\)g, \(l = 30\)cm, \(\kappa = 0.1\) kg/m\(\cdot\)s, \(\Theta_0 = 30°\)
from scipy.integrate import solve_ivp
import numpy as np
theta0 = np.radians(10) # condición inicial
m = 0.1 # masa péndulo (kg)
l = 0.3 # largo del péndulo (m)
K = 0.05 # constante de amortiguación (kg/m*s)
g = 9.8 # gravedad (m/s2)
# Definimos la función F(t,y)
def F(t,y):
return [y[1], # F0(t,y)
- g/l*np.sin(y[0]) - K/(m*l)*y[1]] # F1(t,y)
# Condicion inicial
y0 = np.array([theta0, # posición inicial
0]) # velocidad inicial
t0, tf = (0,5) # tiempo inicial (ti) y final (tf)
# resolvemos la EDO dy/dt = F(t,y)
sol = solve_ivp(fun = F, # Función F(t,y)
t_span = (t0, tf), # Intervalo de tiempo
y0 = y0) # Condición inicial
print(sol)
message: The solver successfully reached the end of the integration interval.
success: True
status: 0
t: [ 0.000e+00 1.753e-04 ... 4.955e+00 5.000e+00]
y: [[ 1.745e-01 1.745e-01 ... -2.589e-03 -2.683e-03]
[ 0.000e+00 -9.942e-04 ... -4.145e-03 -8.792e-05]]
sol: None
t_events: None
y_events: None
nfev: 230
njev: 0
nlu: 0
Notar que la variable sol, tiene una série de atributos que podemos llamar como sol.nombre_atributo, donde nombre_atributo=message, success, status, etc.
La descripción de cada uno de estos atributos está en la documentación oficial de solve_ivp
Las soluciones están en el arreglo sol.y y el paso de tiempo en el arreglo sol.t. Además, debido a que la solución está dada por \(\vec{y} = \left\{\Theta, \dot{\Theta}\right\}\), la variable sol.y es un arreglo de dos filas.
print('Tamaño arreglo t:', sol.t.shape)
print('Tamaño arreglo y:', sol.y.shape)
Tamaño arreglo t: (36,)
Tamaño arreglo y: (2, 36)
Para conocer el ángulo \(\Theta\) y velocidad angular \(\dot{\Theta}\) para algún tiempo \(t\), indexamos los arreglos solt.t y sol.y:
Nota Debido a que la solución está en radianes, usamos
numpy.degreespara convertir a grados.
idx = 30
print('Ángulo en t = %.1fs: %.3f°' % (sol.t[idx], np.degrees(sol.y[0,idx])))
print('Velocidad angular en t = %.1fs: %.3f°/s' % (sol.t[idx], np.degrees(sol.y[1,idx])))
Ángulo en t = 4.3s: 0.148°
Velocidad angular en t = 4.3s: 1.226°/s
Notar, además, que en el input de la función solo indicamos el tiempo inicial y final, pero no especificamos el paso de tiempo \(\Delta t\). Esto es porque, por defecto, solve_ivp busca llegar al valor tf con el menor número de iteraciones.
Así mismo, por defecto, el valor de \(\Delta t\) no es constante y se ajusta en cada iteración.
# comprobamos dt usando numpy.diff
np.diff(sol.t)
array([0.00017528, 0.00175285, 0.01752846, 0.11998446, 0.16456768,
0.1689104 , 0.16219921, 0.14826927, 0.14827456, 0.14679738,
0.1661029 , 0.15676245, 0.17014528, 0.16059003, 0.15220766,
0.15110048, 0.15110048, 0.16655107, 0.15621831, 0.17126165,
0.16138863, 0.15310309, 0.15364646, 0.15364646, 0.1674564 ,
0.15783907, 0.17254208, 0.16525935, 0.15145525, 0.17498422,
0.15800762, 0.16629429, 0.16597964, 0.17287956, 0.04501803])
Graficamos la solución.
%%capture showplot0
import matplotlib.pyplot as plt
# transformamos el ángulo a grados
theta = np.degrees(sol.y[0,:])
theta_dot = np.degrees(sol.y[1,:])
fig, ax = plt.subplots(2,1,figsize=(5,6))
plt.rcParams.update({'font.size': 10}) # Tamaño de fuente
ax[0].plot(sol.t,theta, ':o', label=r'$\Theta(t)$')
ax[1].plot(sol.t,theta_dot, ':o',label=r'$\dot{\Theta}(t)$')
ax[0].set_xlabel('')
ax[0].set_ylabel('$\Theta(t)$ (°)')
ax[1].set_xlabel('Tiempo (s)')
ax[1].set_ylabel('$\dot{\Theta}(t)$ (°/s)')
plt.show()
showplot0()
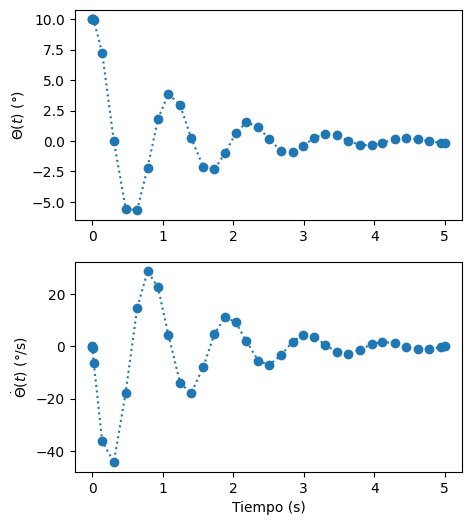
Alternativamente, podemos definir los tiempos donde queremos conocer nuestra solución utilizando el argumento t_eval. Este argumento puede ser un valor específico o un arreglo.
Por ejemplo, consideremos t_eval como un arreglo en el dominio \(t\in[0,5]\) s con \(\Delta t = 0.05\) s.
h = 0.05 # paso de tiempo (s)
t_array = np.arange(0,5,h) # arreglo de tiempos a evaluar
t0, tf = 0, 5 # tiempo inicial (ti) y final (tf)
# Resolvemos la EDO dy/dt = F(t,y)
sol = solve_ivp(fun = F, # Función F(t,y)
t_span = (t0, tf), # Intervalo de tiempo
y0 = y0, # Condición inicial
t_eval = t_array) # Tiempos de evaluación de la solución
%%capture showplot1
import matplotlib.pyplot as plt
# transformamos el ángulo a grados
theta = np.degrees(sol.y[0,:])
theta_dot = np.degrees(sol.y[1,:])
fig, ax = plt.subplots(2,1,figsize=(5,6))
plt.rcParams.update({'font.size': 12}) # Tamaño de fuente
ax[0].plot(sol.t,theta, ':o', label=r'$\Theta(t)$')
ax[1].plot(sol.t,theta_dot, ':o',label=r'$\dot{\Theta}(t)$')
ax[0].set_xlabel('')
ax[0].set_ylabel('$\Theta(t)$ (°)')
ax[1].set_xlabel('Tiempo (s)')
ax[1].set_ylabel('$\dot{\Theta}(t)$ (°/s)')
plt.show()
showplot1()
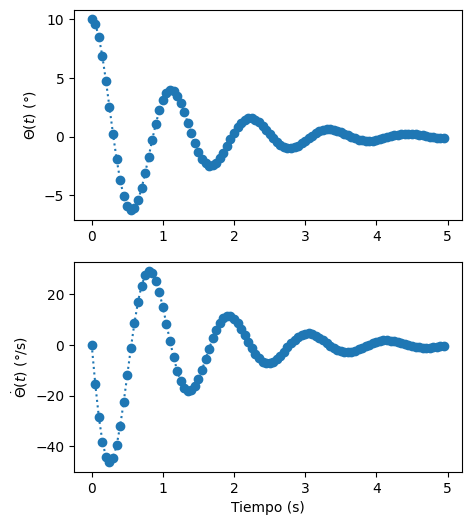
9.6. Rigidez en EDOs#
9.6.1. Rigidez#
Una EDO se define como rígida si una de sus componentes cambia rápidamente respecto a otra. Esto provoca problemas de estabilidad en la solución.
Consideremos por ejemplo la ecuación:
con la condición inicial \(y(0) = 0\)
La solución analítica a esta solución es:
Al analizar la solución observamos que, al comienzo (\(t < 0.005\)), la respuesta está mayormente respresentada por el término transitorio, \(e^{-1000t}\). Luego, la respuesta comienza a ser dominada por el término \(e^{-t}\)
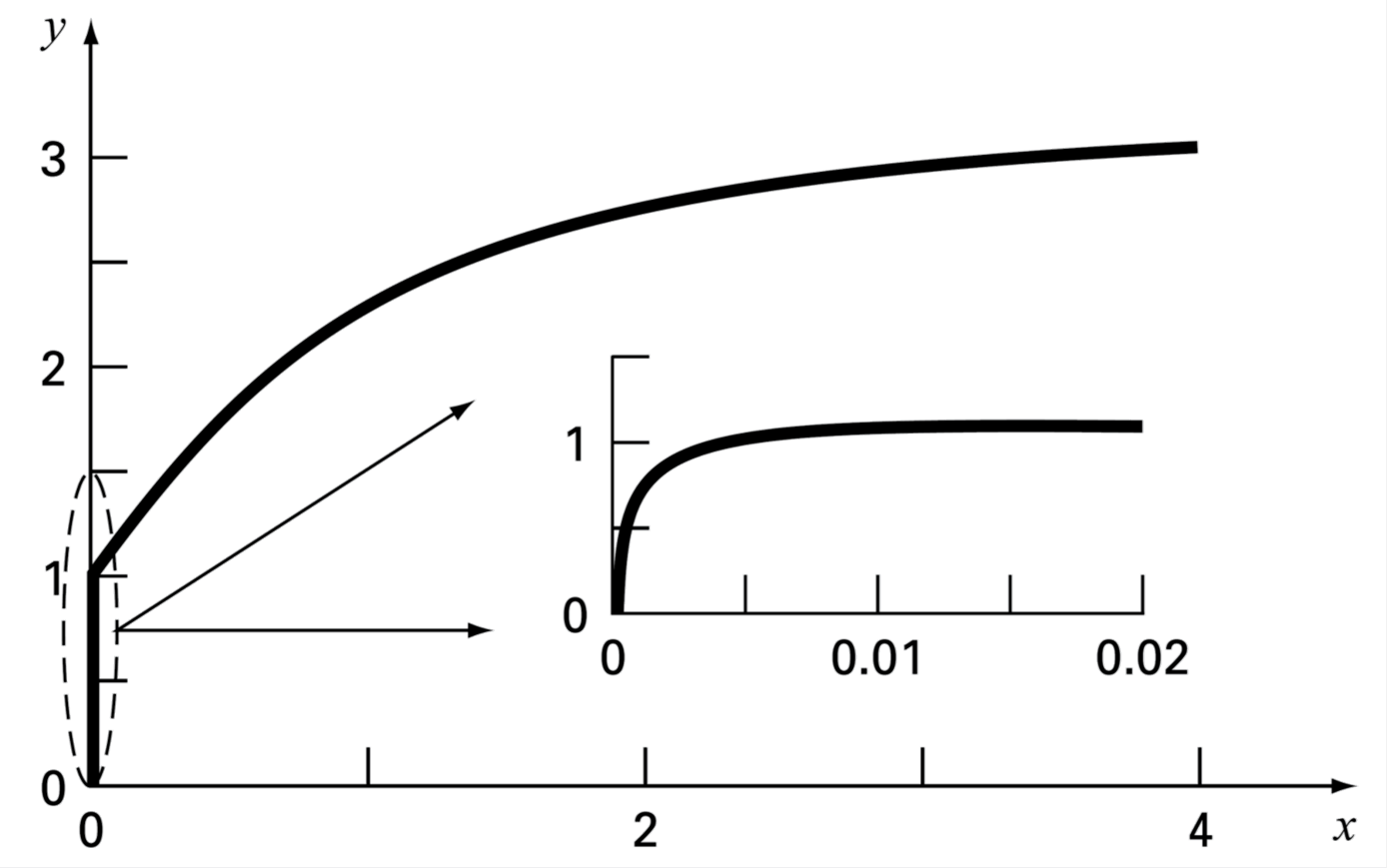
Como el método no conoce la solución analítica, el término transitorio genera problemas de inestabilidad si el valor de \(\Delta t\) es muy grande; o de convergencia, si \(\Delta t\) es muy pequeño.
9.6.2. Recomendaciones#
Para EDOs no rígidas, se recomiendan los métodos
RK45,RK23yDOP853.Para EDOs rígidas, se recomienda los métodos
RadauyBDF.
Como regla general, se recomienda intentar con un método explícito (como RK45). Si la solución diverge o tiene un comportamiento inusual, es probable la EDO sea rígida y, en ese caso, se debe utilizar un método implícito de paso simple (Radau) o multipaso (BDF).
Revisemos esto analizando la siguiente EDO en el intervalo \(t\in[0,10]\):
# Definimos nuestra EDO en código
t0, tf = (0,10) # intervalo de tiempo
F = lambda t,y: - 100000 * (y - np.cos(t)) # función F(t,y)
Compararemos el tiempo de cómputo y el tamaño del arreglo sol.t cuando usamos:
Método de paso simple explícito (
method = RK45)Método de paso simple implícito (
method = Radau)Método de paso múltiple implícito (
method = BDF)
# Usamos method = RK45
%time sol = solve_ivp(fun = F,t_span = (t0, tf), y0 = [1], method = 'RK45')
print('Número de subdivisiones de variable "t": %i' % sol.t.shape[0])
---------------------------------------------------------------------------
KeyboardInterrupt Traceback (most recent call last)
File <timed exec>:1
File ~/miniconda3/lib/python3.11/site-packages/scipy/integrate/_ivp/ivp.py:650, in solve_ivp(fun, t_span, y0, method, t_eval, dense_output, events, vectorized, args, **options)
648 status = None
649 while status is None:
--> 650 message = solver.step()
652 if solver.status == 'finished':
653 status = 0
File ~/miniconda3/lib/python3.11/site-packages/scipy/integrate/_ivp/base.py:197, in OdeSolver.step(self)
195 else:
196 t = self.t
--> 197 success, message = self._step_impl()
199 if not success:
200 self.status = 'failed'
File ~/miniconda3/lib/python3.11/site-packages/scipy/integrate/_ivp/rk.py:147, in RungeKutta._step_impl(self)
144 y_new, f_new = rk_step(self.fun, t, y, self.f, h, self.A,
145 self.B, self.C, self.K)
146 scale = atol + np.maximum(np.abs(y), np.abs(y_new)) * rtol
--> 147 error_norm = self._estimate_error_norm(self.K, h, scale)
149 if error_norm < 1:
150 if error_norm == 0:
File ~/miniconda3/lib/python3.11/site-packages/scipy/integrate/_ivp/rk.py:109, in RungeKutta._estimate_error_norm(self, K, h, scale)
108 def _estimate_error_norm(self, K, h, scale):
--> 109 return norm(self._estimate_error(K, h) / scale)
File ~/miniconda3/lib/python3.11/site-packages/scipy/integrate/_ivp/rk.py:106, in RungeKutta._estimate_error(self, K, h)
105 def _estimate_error(self, K, h):
--> 106 return np.dot(K.T, self.E) * h
File <__array_function__ internals>:177, in dot(*args, **kwargs)
KeyboardInterrupt:
Número de subdivisiones de variable "t": 100
# Usamos method = BDF
%time sol = solve_ivp(fun = F,t_span = (t0, tf), y0 = [1], method = 'BDF')
print('Número de subdivisiones de variable "t": %i' % sol.t.shape[0])
CPU times: user 10.2 ms, sys: 12 µs, total: 10.2 ms
Wall time: 10.4 ms
Número de subdivisiones de variable "t": 56
# Usamos method = Radau
%time sol = solve_ivp(fun = F,t_span = (t0, tf), y0 = [1], method = 'Radau')
print('Número de subdivisiones de variable "t": %i' % sol.t.shape[0])
CPU times: user 4.9 ms, sys: 58 µs, total: 4.96 ms
Wall time: 4.61 ms
Número de subdivisiones de variable "t": 7
Como vemos, el tiempo de cómputo y el número de subdivisiones con los métodos implícitos Radau y BDF es significativamente menor, en comparación con métodos de paso simple (como RK45).
9.7. Referencias#
Kong Q., Siauw T., Bayen A. M. Chapter 22: ODEs Initial-Value Problems in Python Programming and Numerical Methods – A Guide for Engineers and Scientists, 1st Ed., Academic Press, 2021
Chapra S., Canale R. Capítulo 25: Métodos de Runge-Kutta en Métodos Numéricos para Ingenieros, 6ta Ed., McGraw Hill, 2011
Chapra S., Canale R. Capítulo 26: Métodos rígidos y de paso múltiple en Métodos Numéricos para Ingenieros, 6ta Ed., McGraw Hill, 2011
Williams H. P. Chapter 17: Integration of Ordinary Differential Equations in “Numerical Recipes” 3rd Ed, Cambridge University Press, 2007