Series de Taylor

5. Series de Taylor#

5.1. Expansión de funciones en series de Taylor#

La expansión en series de Taylor es una forma alternativa de representar una función mediante una serie infinita de polinomios alrededor de un punto \(a\):

(5.1)#\[\begin{equation} f(x) = \sum_{n = 0}^{\infty} \frac{f^{(n)}(a)(x-a)^n}{n!} \end{equation}\]

donde \(f^{(n)}\) es la \(n\)-ésima derivada de \(f\), con \(f^{(0)} = f\)

Por ejemplo, derivemos la expansión en series de Taylor de la función \(f(x) = 5x^2 + 3x + 5\) alrededor del punto \(a = 0\).

Primero, determinamos la forma de cada derivada:

\[\begin{eqnarray*} f(x) &=& 5x^2 + 3x + 5\\ f'(x) &=& 10x + 3\\ f''(x) &=& 10 \\ f'''(x) &=& 0 \\ \end{eqnarray*}\]

Luego, evaluamos cada derivada en el punto \(a = 0\), y reemplazamos en la fórmula:

\[\begin{align*} f(x) &= \frac{1}{0!}(5a^2 + 3a + 5)(x - a)^0 + \frac{1}{1!}(10a + 3)(x - a)^1 + \frac{1}{2!}(10)(x - a)^2 + 0 + 0 + \cdots\\ &= \frac{5x^0}{0!} + \frac{3x^1}{1!} + \frac{10x^2}{2!} \\ &= 5x^2 + 3x + 5 \end{align*}\]

Si ahora, por ejemplo, derivamos la expansión de Taylor para \(a = 2\):

\[\begin{align*} f(x) &= \frac{1}{0!}[5(2)^2 + 3(2) + 5](x - 2)^0 + \frac{1}{1!}[10(2) + 3](x - 2)^1 + \frac{1}{2!}(10)(x - 2)^2 + 0 + 0 + \cdots\\ &= \frac{31(x-2)^0}{0!} + \frac{23(x-2)^1}{1!} + \frac{10(x-2)^2}{2!} = 31 + 23x - 46 + 5x^2 - 20x + 20 \\ &= 5x^2 + 3x + 5 \end{align*}\]

Como cololario general tenemos que una expansión de Taylor de un polinomio siempre es el mismo polinomio

5.2. Aproximaciones mediante series de Taylor#

Para funciones no polinomiales, las series de Taylor continene infinitos términos.

Por ejemplo, la expansión de Taylor de \(f(x) = \sin(x)\) alrededor de \(a=0\):

\[\begin{align*} f(x) &= \frac{\sin(0)}{0!}x^0 + \frac{\cos(0)}{1!}x^1 + \frac{-\sin(0)}{2!}x^2 + \frac{-\cos(0)}{3!}x^3 + \frac{\sin(0)}{4!}x^4 + \frac{\cos(0)}{5!}x^5 + \cdots \\ &= \frac{1}{1!}x^1 - \frac{1}{3!}x^3 + \frac{1}{5!}x^5 + \cdots \\ \end{align*}\]

Analizando el patrón de la serie, tenemos que:

\[\begin{equation*} \sin(x) = \sum_{n = 0}^{\infty} \frac{(-1)^n x^{2n+1}}{(2n+1)!} \end{equation*}\]

La ventaja de la representación en series de Taylor cobra relevancia cuando buscamos evaluar esta función computacionalmente. Esto debido a que un cálculo en base a polinomios solo requiere de operaciones básicas, como sumar, restar, multiplicar y dividir.

Si bien, matemáticamente, la serie esta definida por infinitos términos, es posible obtener una buena aproximación considerando un número finito de ellos. Es decir, aproximamos la función truncando la serie de Taylor

\[\begin{equation*} \sin(x) \approx \sum_{n = 0}^{N} \frac{(-1)^n x^{2n+1}}{(2n+1)!} \end{equation*}\]

Decimos que la aproximación de una función es de orden \(N\) cuando la serie considera hasta el término \(N\) de la serie de Taylor

A mayor orden, mejor la aproximación

Analicemos esto en un código, a partir de la expansión de la función \(f(x) = \sin(x)\)

%%capture showplot
import numpy as np
import math    # para generar número factorial
import matplotlib.pyplot as plt

x = np.linspace(-np.pi, np.pi, 200)
y = np.zeros_like(x)

plt.figure(figsize = (7, 4))           # Tamaño de figura
plt.rcParams.update({'font.size': 10}) # Tamaño de fuente

for n in range(4):
    y += (-1)**n*x**(2*n+1)/math.factorial(2*n+1)    # serie de taylor
    plt.plot(x,y, '-', label = ('Orden %i' % (2*(n + 1)))) # graficamos serie de taylor

plt.plot(x, np.sin(x), 'k', label = r'$\sin(x)$', lw = 4)
plt.grid()
plt.title('Aproximación de sin(x) en series de Taylor (a = 0)')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.ylim(-2,2)
plt.show()

showplot()
../_images/352db24f1ad24a706ecfe7196ab12fa3a680dd162fac4e495600c5ae7801dcdd.png

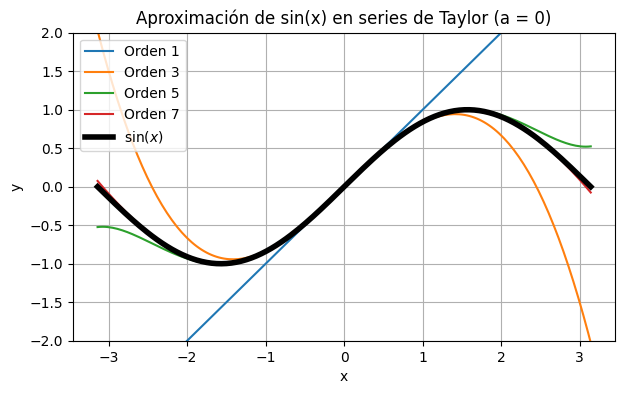
El grafico muestra como la aproximación de \(\sin(x)\) mejora alrededor del punto \(x = 0\), a medida que aumentamos el orden. Para el orden 8, la aproximación es casi perfecta en todo el dominio \(x\in [-\pi,\pi]\)

Comúnmente, los métodos numéricos utilizan la aproximación de primer orden, también denominada aproximación lineal. Esto debido a que la aproximación lineal es suficientemente buena en valores cercanos a “\(a\)”.

En otras palabras, una función siempre se verá lineal si la vemos desde suficientemente cerca.

5.3. Analisis de errores en series de Taylor#

5.3.1. Errores de truncamiento#

En la primera clase hablamos de los errores de redondeo inducidos por la capacidad limitada de un computador de almacenar los decimales de un número. Cuando aproximamos una función por una serie de orden \(N\), estamos induciendo un error de truncamiento.

Por ejemplo, la expansión de la función \(e^x\) en series de Taylor centrada en \(x=0\) está dada por:

\[\begin{equation*} e^x = 1+x+\frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + \dots \end{equation*}\]

Analicemos el error de truncamiento para \(e^2\), asociado al orden \(N\) de la aproximación.

En este caso, la serie truncada es:

\[\begin{equation*} e^x \approx \sum_{n = 0}^N \frac{x^n}{n!} \end{equation*}\]
x = 2.0 # evaluamos la función exp(2)
N = 9

exp_approx = 0 # valor inicial
for n in range(N + 1):
    exp_approx += ((x**n)/math.factorial(n))
    print('Error aprox. orden %i: %.5f' %  (n ,np.abs(exp_approx - np.exp(2))))

Error aprox. orden 0: 6.38906
Error aprox. orden 1: 4.38906
Error aprox. orden 2: 2.38906
Error aprox. orden 3: 1.05572
Error aprox. orden 4: 0.38906
Error aprox. orden 5: 0.12239
Error aprox. orden 6: 0.03350
Error aprox. orden 7: 0.00810
Error aprox. orden 8: 0.00175
Error aprox. orden 9: 0.00034

5.4. Errores de redondeo#

Es importante notar que debido a que una serie de Taylor se calcula mediante la suma susesiva de términos, esto puede generar errores de redondeo. Generalmente, el error es más evidente cuando el valor exacto es pequeño.

Por ejemplo, consideremos la aproximación de \(e^{-30}\) usando 200 términos de la serie.

exp = 0
x = -30
for i in range(4+1):
    exp += ((x**i)/math.factorial(i))
print('El valor de e^(-30)')    
print('... Aproximación de orden %i: %.5e' % (i,exp))    
print('... Valor exacto: %.5e' % np.exp(x))

El valor de e^(-30)
... Aproximación de orden 4: 2.96710e+04
... Valor exacto: 9.35762e-14

A partir de este ejemplo podemos ver que, producto del error de redondeo, nuestra estimación de \(e^{-30}\) es erronea, a pesar de haber incluído 200 términos de la serie.

5.5. Referencias#

Contents